Закон збереження моменту імпульсу
Закон збереження моменту імпульсу: момент імпульсу замкненої системи відносно будь-якої нерухомої точки не змінюється з часом, тобто
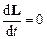 і
і 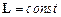 .
.
Відповідно, момент імпульсу замкненої системи відносно його центра інерції не змінюється з часом:
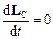 і
і 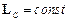 .
.
Подібно до законів збереження імпульсу та енергії, закон збереження моменту імпульсу далеко виходить за рамки класичної механіки. Він належить до ряду найфундаментальніших фізичних законів, оскільки пов’язаний із певною властивістю симетрії простору – його ізотропністю. Ізотропність простору проявляється в тому, що фізичні властивості та закони руху замкненої системи не залежать від вибору напрямку осей координат інерціальної системи відліку, тобто не змінюються при повороті в просторі замкненої системи як цілого на будь-який кут.
Згідно з сучасними уявленнями, момент імпульсу можуть мати не тільки частинки та тіла, але також і поля, причому елементарні частинки і побудовані з них системи (наприклад, атомні ядра) можуть мати момент імпульсу, не пов’язаний із рухом цих частинок у просторі, і який називається їх спіном.
Стосовно систем, які описуються класичною (ньютонівською) механікою, закон збереження моменту імпульсу можна розглядати як наслідок законів Ньютона. Для замкненої механічної системи головний момент зовнішніх сил відносно будь-якої нерухомої точки (а також відносно центра інерції системи) тотожно дорівнює нулю: 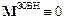 (відповідно
(відповідно 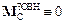 , де
, де 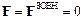 ), звідки випливає закон збереження моменту імпульсу:
), звідки випливає закон збереження моменту імпульсу:
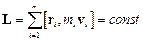 ,
,
де 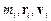 – відповідно маса, радіус-вектор і швидкість і-ї матеріальної точки системи, що складається з n таких точок,
– відповідно маса, радіус-вектор і швидкість і-ї матеріальної точки системи, що складається з n таких точок,
або
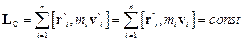 ,
,
де 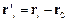 ,
, 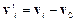 , а
, а 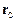 і
і  – відповідно радіус-вектор і швидкість центра інерції системи.
– відповідно радіус-вектор і швидкість центра інерції системи.
Якщо система не замкнена, але діючі на неї зовнішні сили такі, що їх момент відносно нерухомої точки О тотожно рівний нулеві ( 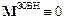 ), то, згідно з законами Ньютона, момент імпульсу системи відносно тієї ж точки О не змінюється з часом:
), то, згідно з законами Ньютона, момент імпульсу системи відносно тієї ж точки О не змінюється з часом: 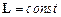 . Цю умову практично задовольняє, наприклад, зрівноважений гіроскоп із трьома ступенями вільності, момент сил тертя в підвісі якого достатньо малий. При будь-яких поворотах підставки такого гіроскопа, яка утримує в стані спокою його центр підвісу, вісь гіроскопа зберігає свою орієнтацію відносно нерухомої інерціальної системи відліку. (Тут покладається, що вектор
. Цю умову практично задовольняє, наприклад, зрівноважений гіроскоп із трьома ступенями вільності, момент сил тертя в підвісі якого достатньо малий. При будь-яких поворотах підставки такого гіроскопа, яка утримує в стані спокою його центр підвісу, вісь гіроскопа зберігає свою орієнтацію відносно нерухомої інерціальної системи відліку. (Тут покладається, що вектор 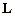 спрямований по осі гіроскопа. У супротивному випадку вільний гіроскоп здійснює регулярну прецесію: його вісь описує колову конічну поверхню, вершина якої знаходиться в центрі підвісу, а вісь напрямлена вздовж вектора
спрямований по осі гіроскопа. У супротивному випадку вільний гіроскоп здійснює регулярну прецесію: його вісь описує колову конічну поверхню, вершина якої знаходиться в центрі підвісу, а вісь напрямлена вздовж вектора 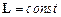 ).
).
Зазвичай 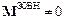 і
і 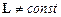 . Втім, якщо головний момент зовнішніх сил відносно якоїсь нерухомої осі, що проходить через точку О, тотожно рівний нулеві, то момент імпульсу системи відносно цієї осі не змінюється з часом. Наприклад, якщо
. Втім, якщо головний момент зовнішніх сил відносно якоїсь нерухомої осі, що проходить через точку О, тотожно рівний нулеві, то момент імпульсу системи відносно цієї осі не змінюється з часом. Наприклад, якщо 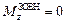 , то
, то 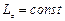 .
.
У випадку, коли система обертається навколо нерухомої осі OZ, а головний момент зовнішніх сил відносно цієї осі 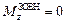 , момент імпульсу системи відносно осі обертання не змінюється з часом:
, момент імпульсу системи відносно осі обертання не змінюється з часом:
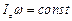 ,
,
де 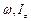 – відповідно кутова швидкість і момент інерції системи.
– відповідно кутова швидкість і момент інерції системи.
Якщо під дією внутрішніх сил, а також зовнішніх сил, які задовольняють умову 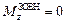 , система деформується і її момент інерції Iz змінюється, то відповідно зростає або спадає кутова швидкість
, система деформується і її момент інерції Iz змінюється, то відповідно зростає або спадає кутова швидкість 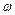 . Яскравий тому приклад можна побачити під час змагань з фігурного катання на ковзанах: коли спортсмен притискає до себе руки під час обертання навколо вертикальної осі, кутова швидкість його обертання помітно зростає.
. Яскравий тому приклад можна побачити під час змагань з фігурного катання на ковзанах: коли спортсмен притискає до себе руки під час обертання навколо вертикальної осі, кутова швидкість його обертання помітно зростає.
Вільними осями тіла називаються такі осі, навколо яких вільне тверде тіло може обертатися зі сталою кутовою швидкістю (за відсутності будь-яких зовнішніх впливів). Таке обертання тіла називається інерційним, або вільним, обертанням. Вільні осі тіла збігаються з його головними центральними осями інерції. У загальному випадку значення 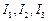 головних центральних моментів інерції тіла різні. Вільне обертання такого тіла (наприклад, однорідного прямокутного паралелепіпеда з різнодовжинними ребрами) практично здійснюється тільки навколо двох вільних осей, які відповідають екстремальним значенням головних центральних моментів інерції – найбільшому і найменшому. Обертання тіла навколо його третьої головної центральної осі, яка відповідає проміжному значенню моменту інерції тіла, нестійке: навіть малі зовнішні впливи можуть спричиняти значні відхилення миттєвої осі обертання тіла від її первісного напрямку в тілі.
головних центральних моментів інерції тіла різні. Вільне обертання такого тіла (наприклад, однорідного прямокутного паралелепіпеда з різнодовжинними ребрами) практично здійснюється тільки навколо двох вільних осей, які відповідають екстремальним значенням головних центральних моментів інерції – найбільшому і найменшому. Обертання тіла навколо його третьої головної центральної осі, яка відповідає проміжному значенню моменту інерції тіла, нестійке: навіть малі зовнішні впливи можуть спричиняти значні відхилення миттєвої осі обертання тіла від її первісного напрямку в тілі.
Якщо значення двох головних центральних моментів інерції тіла однакові, 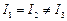 , то стійке вільне обертання такого тіла (наприклад, однорідного кругового циліндра) можливе тільки навколо тієї вільної осі, яка відповідає відмінному від них третьому значенню моменту інерції тіла
, то стійке вільне обертання такого тіла (наприклад, однорідного кругового циліндра) можливе тільки навколо тієї вільної осі, яка відповідає відмінному від них третьому значенню моменту інерції тіла 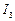 . Для однорідного кругового циліндра такою вільною віссю є його вісь симетрії. Проте, якщо довгий і тонкий циліндр здійснює обертальний рух за допомогою прикріпленої до його кінця нитки, то стійким виявляється обертання циліндра навколо тої вільної осі, яка відповідає найбільшому значенню його моменту інерції. Ця вільна вісь перпендикулярна до осі співпоміру циліндра.
. Для однорідного кругового циліндра такою вільною віссю є його вісь симетрії. Проте, якщо довгий і тонкий циліндр здійснює обертальний рух за допомогою прикріпленої до його кінця нитки, то стійким виявляється обертання циліндра навколо тої вільної осі, яка відповідає найбільшому значенню його моменту інерції. Ця вільна вісь перпендикулярна до осі співпоміру циліндра.
Приклад застосування закону збереження моменту імпульса. Розглянемо ще один приклад балістичного маятника (рис.4.6). Однорідний стержень маси 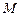 довжини
довжини 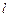 шарнірно підвішений у точці О. У нижній кінець стержня потрапляє і застряє там куля маси
шарнірно підвішений у точці О. У нижній кінець стержня потрапляє і застряє там куля маси 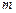 . У результаті стержень повертається на кут
. У результаті стержень повертається на кут 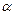 . Користуючись законами збереження, потрібно визначити зв’язок між кутом відхилення
. Користуючись законами збереження, потрібно визначити зв’язок між кутом відхилення 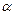 і швидкістю кулі
і швидкістю кулі 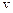 .
.
Розглядувана механічна система – стержень плюс куля – незамкнена, оскільки на тіла діють зовнішні сили. На відміну від розглянутого раніше прикладу балістичного маятника, у даному випадку горизонтальна складова імпульсу системи не зберігається, оскільки сили реакції, що виникають у точці підвісу, мають горизонтальну складову як під час повороту стержня, так і під час удару кулі. (До речі, ці сили реакції можна відчути навіть у повсякденному житті. Якщо взяти стержень за кінець у руку і стукнути іншим кінцем стержня об землю, то сили реакції будуть істотно відчутні.) Отже, закон збереження імпульсу ми застосувати не можемо. Залишаються закони збереження енергії і моменту імпульсу.
Розглянемо момент імпульса системи відносно осі, що проходить через точку О перпендикулярно до площини малюнка, у момент часу 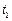 (до удару) і у момент часу
(до удару) і у момент часу 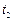 (безпосередньо після удару, коли куля вже застрягла у стержні, але стержень ще не встиг повернутись на помітний кут). Оскільки на інтервалі
(безпосередньо після удару, коли куля вже застрягла у стержні, але стержень ще не встиг повернутись на помітний кут). Оскільки на інтервалі 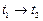 усі зовнішні сили мають нульовий момент відносно обраної осі, можна застосувати закон збереження моменту імпульсу
усі зовнішні сили мають нульовий момент відносно обраної осі, можна застосувати закон збереження моменту імпульсу
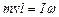 ,
,
де  - момент інерції стержня відносно осі О,
- момент інерції стержня відносно осі О, 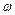 - початкова кутова швидкість обертання стержня.
- початкова кутова швидкість обертання стержня.
Закон збереження енергії застосуємо так само, як це було зроблено у попередньому прикладі балістичного маятника. Кінетична енергія обертального руху стержня у момент часу 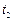 дорівнює його потенціальній енергії у момент максимального відхилення
дорівнює його потенціальній енергії у момент максимального відхилення
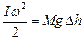 ,
,
де 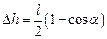 - вертикальне зміщення центру мас стержня при відхиленні на кут
- вертикальне зміщення центру мас стержня при відхиленні на кут 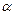 . Шляхом нескладних перетворень з двох вищенаведених рівнянь отримаємо шуканий вираз
. Шляхом нескладних перетворень з двох вищенаведених рівнянь отримаємо шуканий вираз
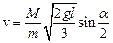 .
.
Дата добавления: 2015-04-07; просмотров: 9336;
