Перетворення Лоренца
Із постулатів спеціальної теорії відносності, а також із однорідності та ізотропності (рівнозворотності) простору і однорідності часу випливає, що співвідношення між координатами і часом однієї й тієї ж події в двох інерційних системах відліку виражається перетвореннями Лоренца, а не перетвореннями Галілея, як це вважається в класичній (ньютонівській) механіці. Згідно з принципом відносності та вищезгаданими властивостями симетрії простору й часу, перетворення Лоренца повинні бути лінійними.
Перетворення Лоренца мають найпростіший вигляд у тому випадку, коли відповідні осі декартових координат нерухомої (К) і рухомої (К`) інерційних систем попарно паралельні (сулежні), причому система К` рухається відносно К зі сталою швидкістю V вздовж осі ОХ. Якщо, крім того, як початок відліку в обох системах (t = 0 і t` = 0) вибраний той момент, коли початки координат О та О` обох систем відліку збігаються, то перетворення Лоренца мають вигляд:
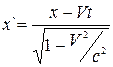 ,
, 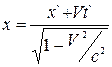
y` = y , y = y`
z` = z , z = z`
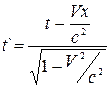 ,
, 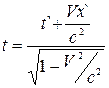 ,
,
де с – швидкість світла у вакуумі.
Перетворення Лоренца показують, що при переході від однієї інерційної системи відліку до другої змінюються не тільки просторові координати розглядуваних подій, але й відповідні їм моменти часу. Проте між просторовими координатами x`, y`, z` події і часом t` її здійснення в довільній інерційній системі відліку К` існує певний взаємозвя’зок, так що величина [(x`)2 + (y`)2 + (z`)2 – c2(t`)2] не залежить від швидкості V системи К`, тобто є однаковою в усіх інерційних системах відліку:
(x`)2 + (y`)2 + (z`)2 – c2(t`)2 = x2 + y2 + z2 – c2t2
Координата x` і час t` не можуть бути уявними. Тому з перетворень Лоренца випливає, що швидкість відносного руху будь-яких двох інерційних систем відліку не може перевищувати швидкість світла у вакуумі (V << c).
Відповідно до принципу відносності Ейнштейна, фізичні закони повинні задовольняти умову релятивістської інваріантності (Лоренц-інваріантності). Ця вимога означає таке: рівняння, що виражають фізичні закони, повинні зберігати свою форму при переході від однієї інерційної системи відліку до іншої, який відбувається згідно з перетвореннями Лоренца.
Перетворення Лоренца переходять у перетворення Галілея при V << c, або, точніше, у границі при V / c ® 0, тобто при c ® ¥. Іншими словами, перетворення Галілея і заснована на них класична (ньютонівська) механіка побудовані на припущенні про миттєве розповсюдження взаємодій. Такий наближений підхід допустимий лише при розгляді закономірностей механічного руху тіл зі швидкостями, значно меншими за швидкість світла у вакуумі.
Дата добавления: 2015-04-07; просмотров: 1384;
