Перетворення швидкостей і прискорень у релятивістській кінематиці

Значення v і v` швидкості матеріальної точки в двох інерційних системах відліку К і К¢ дорівнюють:

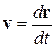= v_xi +v_yj + v_zk, 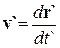= v`_xi` +v`_yj` + v`_zk` ,

де r = x i +y j+ z kі r` = x` i` +y` j`+ z` k` – радіуси-вектори декартових координат систем відліку К і К¢. Проекції швидкостей v і v` на осі декартових координат дорівнюють:

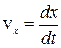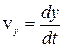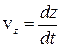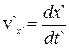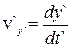, , , , , і .

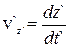Якщо відповідні осі декартових координат систем відліку К¢ і К попарно паралельні і система К¢ рухається відносно К зі сталою швидкістю V, напрямленою вздовж осі ОХ, притому в момент початку відліку часу в К і К¢ (t=0 і t`=0) початки координат О і О¢ цих систем відліку збігаються. З перетворень Лоренца випливає, що зв’язок між проекціями точки на осі декартових координат в системах К і К¢ має вигляд:

, ,

, .

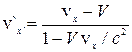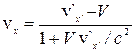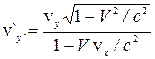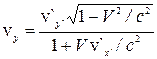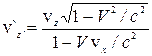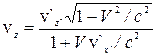Ці формули виражають закон складання швидкостей у релятивістській кінематиці. У границі при с®¥ вони призводять до звичайного закону складання швидкостей у класичній механіці (2.8.2):

v`_x` = v_x – V, v`_y` = v_y, v`_z` = v_z і v` = v – V.

Зв’язок між квадратами модулів векторів v і v`

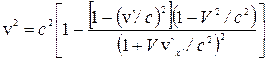і .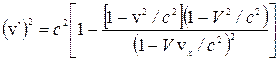

Зокрема, якщо v` = c, то v = c і навпаки. Отже, якщо швидкість частинки відносно якої-небудь інерційної системи відліку дорівнює швидкості світла у вакуумі, то вона повинна бути такою ж за величиною відносно будь-якої іншої інерційної системи відліку незалежно від швидкості відносного руху цих систем відліку. Інакше кажучи, сума двох швидкостей, із яких одна рівна с, завжди дорівнює с. У цій закономірності, яка виявляється при русі таких елементарних частинок, як фотони і нейтрино, проявляється граничний характер швидкості світла у вакуумі.

Із отриманих співвідношень видно, що частинка, яка рухається відносно якої-небудь інерційної системи відліку з меншою від с швидкістю, має швидкість відносно будь-якої іншої інерційної системи відліку теж меншу від с (наприклад, якщо v < c , то v` < c, і навпаки). Звідси, зокрема, випливає, що якими б не були близькими до с швидкості двох частинок, їх відносна швидкість завжди менша за с. Наприклад, нехай дві частинки рухаються вздовж осі ОХ системи відліку К зі швидкостями, відповідно рівними v₁= 0,8ci і v₂= – 0,8ci. Швидкість u₂₁ другої частинки відносно першої не дорівнює, як це вважається в класичній механіці, геометричній різниці v₂– v₁= – 1,6ci хоча б тому, що модуль цієї швидкості переважає с. Шукана швидкість дорівнює швидкості другої частинки відносно інерційної системи відліку К¢, яка рухається разом із першою частинкою (V = 0,8ci), тобто u₂₁=v`₂.

Із наведених вище формул випливає, що

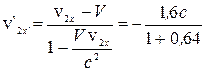= -0,976с, 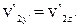= 0,

тобто u₂₁=–0,976ci і ½u₂₁½< c.

Проекції прискорення матеріальної точки на осі декартових координат двох інерційних систем відліку К і К¢, пов¢язані між собою такими співвідношеннями:

<28 29 303132 33 34 >

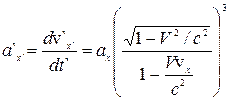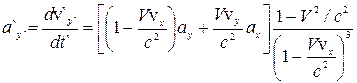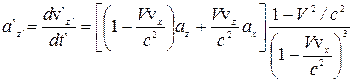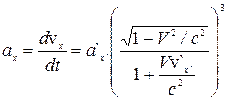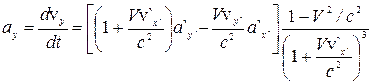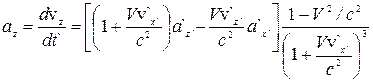Дата добавления: 2015-04-07; просмотров: 1249;