Основний закон релятивістської динаміки

У класичній (ньютонівській) механіці вважалось, що маса тіла має одне і те саме значення в різних інерційних системах відліку. Досліди над тілами, швидкість руху яких менша за швидкість світла, підтверджували таке припущення. Проте, відношення 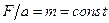справедливе лише при достатньо невеликих швидкостях. Якщо швидкості тіл зростають, то це співвідношення починає зростати зі швидкістю. У релятивістській механіці, на відміну від класичної, маса матеріальної точки не є сталою, а залежить від швидкості v цієї точки. Її значення m різне в двох інерційних системах відліку, що рухаються одна відносно іншої. Залежність маси від швидкості виражається формулою:

,

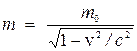де m₀ – маса спокою частинки (матеріальної точки), тобто її маса, виміряна в тій інерційній системі відліку, відносно якої частинка перебуває в спокої, с – швидкість світла у вакуумі. Масу m часто називають релятивістською масою. Іншими словами, маса однієї ї тієї самої частинки різна в різних неінерційних системах відліку. На відміну від релятивістської маси маса спокою частинки m₀ є інваріантною величиною, тобто вона є однаковою в різних системах відліку.

Вплив швидкості частинки на величину її релятивістської маси стає суттєвим тільки при значеннях v, близьких до с. Наприклад, m/m₀ = 1,005 при v/c = 0,1 і m/m₀ = 2,29 при v/c = 0,9. Із закону залежності m від v видно, що частинки з масою спокою m₀ не можуть рухатися зі швидкостями, більшими чи рівними с (v<c). У той же час частинки, маса спокою яких дорівнює нулю (фотони та нейтрино), не можуть мати швидкість, відмінну від с.

За аналогією з класичною механікою вводиться імпульс релятивістської частинки:

,

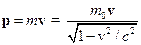який є нелінійною функцією її швидкості.

Вектор p іноді називають релятивістським імпульсом матеріальної точки (на відміну від значення m₀v її імпульсу в класичній механіці). Імпульс m₀v,який вводивсяв класичній механіці, не зберігається для замкненої системи релятивістських частинок. В результаті, виникла альтернатива: або відмовитися від класичного означення імпульсу або від закону збереження цієї величини. Закони збереження відіграють дуже важливу роль в природі, тому в теорії відносності за фундаментальний беруть саме закон збереження імпульсу, і виходячи з цього знаходять вираз для самого імпульсу. Дослід показує, що саме релятивістський імпульс частинки, введений в описаним вище способом, підкоряється закону збереження імпульсу незалежно від вибору інерційної системи відліку. Очевидно, що при v<<c імпульс p = mv» m₀v.

Внаслідок однорідності простору у релятивістській механіці справедливим є закон збереження релятивістського імпульсу: імпульс замкненої системи не змінюється з часом.

Із цього закону випливає закон збереження релятивістської маси: при будь-яких процесах, які відбуваються в замкненій системі, її повна релятивістська маса не змінюється.

За принципом відносності Ейнштейна, всі закони природи мають бути однакові в різних інерційних системах відліку. Тобто, математичні формулювання фізичних законів повинні мати однаковий вигляд в різних інерційних системах відліку. Це має стосуватись і динаміки. Але, як показує ретельний аналіз, основне рівняння динаміки Ньютона 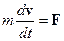не узгоджується з принципом відносності. Перетворення Лоренца, які застосовуються при переході до іншої інерційної системи відліку, надають основному рівнянню динаміки зовсім іншу форму. Очевидно, основне рівняння динаміки в релятивістському випадку повинно мати інший вигляд, і лише при v<<c переходити в ньютонівське рівняння. Таким вимогам відповідає рівняння, яке назвали основним законом релятивістської динаміки: швидкість зміни релятивістського імпульсу матеріальної точки дорівнює силі F, яка діє на цю точку, тобто

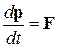, або .

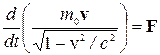Примітка. Якщо на матеріальну точку одночасно діють кілька сил, то під силою F треба розуміти рівнодійну силу.

Елементарна робота сили F на малому переміщенні dr точки її прикладання dA = (F dr) = (Fv) dt.

Із основного закону релятивістської динаміки і формули залежності маси від швидкості випливає, що

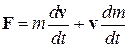і .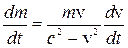

Тому

dA = (Fv) dt = m (vdv) + v² dm = mvdv + v² dm = c² dm.

Прискорення, яке сила F надає матеріальній точці,

.

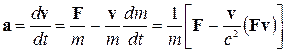Таким чином, на відміну від класичної механіки, в релятивістській механіці прискорення матеріальної точки, взагалі кажучи, не збігається за напрямком із силою, яка його спричиняє. Вектор а колінеарний силі F тільки в двох випадках:

а) сила F спрямована перпендикулярно до швидкості v точки (поперечна сила), так що (Fv) = 0 і

;

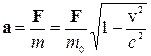б) сила F напрямлена паралельно вектору v швидкості точки (поздовжна сила), так що v(Fv) = v²F і

.

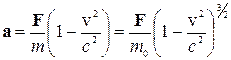Поздовжна сила надає матеріальній точці прискорення у (1–v²/c²) ^–1 разів менше, ніж така ж за величиною поперечна сила. Це пов¢язано з тим, що поперечна сила зумовлює зміну швидкості точки тільки за напрямком (модуль швидкості і релятивістська маса точки не змінюються), а поздовжна сила спричиняє зміну значення модуля швидкості точки та її маси. Якщо швидкість частинки близька до релятивістської, то для зміни абсолютного значення її швидкості треба прикласти значно більшу силу, ніж для зміни її напрямку. Тобто, дуже швидка частинка легше змінює напрямок швидкості, ніж її абсолютне значення.