Відносність довжин і проміжків часу. Інтервал між двома подіями

Із перетворень Лоренца випливає, що лінійний розмір тіла, яке рухається відносно інерційної системи відліку, зменшується в напрямку руху. Ця зміна поздовжного розміру тіла при його русі називаться лоренцовим скороченням. Нехай l₀ – довжина стержня, що перебуває в стані спокою в системі відліку К`. Якщо стержень розташований вздовж осі O`X` (рис. 5.2), то l<sub>0</sub> = x<sub>2</sub>` – x₁`, де x<sub>2</sub>` і x₁` – координати кінців стержня. Довжина l того ж стержня в системі відліку К, відносно якого він рухається вздовж осі ОХ зі швидкістю V, дорівнює різниці значень координат кінців стержня, виміряних в один і той же момент часу t:

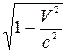l = x₂(t) – x₁(t) = (x₂`– x<sub>2</sub>`) = l₀ .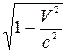

Поперечні розміри тіла не залежать від швидкості його руху і однакові в усіх інерційних системах відліку:

y₂ – y₁ = y`<sub>2</sub> – y`₁ і z₂ – z₁ = z`<sub>2</sub> – z`₁.

Отже, лінійні розміри тіла відносні. Вони максимальні в тій самій інерційній системі відліку, відносно якої тіло перебуває в спокої. Ці розміри тіла називаються його власними розмірами.

Лоренцеве скорочення є кінематичним ефектом спеціальної теорії відносності. Воно не пов’язане з дією на тіло якихось поздовжніх сил, які стискають його вздовж напрямку руху. Це скорочення помітне тільки при швидкостях руху, близьких до швидкості світла у вакуумі. Із формули для лоренцевого скорочення випливає, що тіла не можуть рухатися зі швидкостями V ³ c , бо при V = c поздовжній розмір тіла обертається в нуль, а при V > c він повинен стати уявним.

Із перетворень Лоренца видно, що в теорії відносності можна говорити про певний “момент часу” лише стосовно якої-небудь одної певної інерційної системи відліку. Так, наприклад, одному “моменту часу” в системі відліку К (одному певному значенню часу t в цій системі) відповідає множина значень часу t` в системі відліку К` залежно від значень координати х:

.

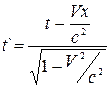Навпаки, одному “моменту часу” в системі відліку К`, тобто одному певному значенню часу t`, відповідає множина значень часу t в системі відліку К залежно від значень координати х`:

.

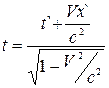Ще один важливий наслідок перетворень Лоренца – відносність проміжку часу між якими-небудь двома подіями (наприклад, між початком і кінцем якого-небудь процесу), тобто залежність цього проміжку від вибору інерційної системи відліку. Нехай у рухомій інерційній системі відліку К` дві розглядувані події 1 і 2 відбуваються в одній і тій же нерухомій відносно К` точці А (x`<sub>2</sub> = x`₁) в моменти часу t`<sub>1</sub> і t`₂ , так що проміжок часу між цими подіями t = t`<sub>2</sub> – t`₁.

Відносно нерухомої інерційної системи відліку К точка А рухається з тією ж швидкістю V, що й система К`. Тому в К події 1 і 2 відбуваються в різних точках простору з координатами x₁ і x₂, причому x₂ – x₁ = Vt, де t = t₂ – t₁ – проміжок часу між подіями 1 і 2 за годинником у системі відліку К. Із перетворень Лоренца випливає, що

t = t₂ – t₁ = .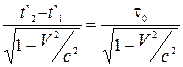

Таким чином, проміжок часу між двома подіями мінімальний у тій системі відліку, відносно якої обидві події відбуваються в одній і тій же точці. Час, вимірюваний за годинником, який рухається разом із даним об’єктом, називається власним часом цього об’єкта.

Розглянуті закономірності свідчать про існування релятивістського ефекту сповільнення ходу часу в рухомій інерційній системі відліку порівняно з нерухомою. Годинник, який рухається зі швидкістю відносно даної інерційної системи відліку, йде повільніше в 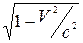разів, ніж нерухомий. Відповідно, за принципом відносності, всі фізичні процеси в рухомій системі відліку відбуваються повільніше, ніж у нерухомій.

Ефект сповільнення ходу часу стає помітним тільки при дуже великих швидкостях руху V, близьких до швидкості світла у вакуумі. Він підтверджується експериментально, наприклад, у дослідах із мюонами. Мюон – нестабільна елементарна частинка. Середній власний час життя мюона (за годинником у тій інерційній системі відліку, відносно якої він перебуває в спокої) t₀ = 2.2×10^-6 с . Мюони народжуються у верхніх шарах атмосфери під дією первинного космічного проміння і рухаються відносно Землі зі швидкостями V, близькими до с. Якби релятивістського ефекту сповільнення ходу часу не було, то відносно земного спостерігача мюон міг би пройти за час свого життя шлях в атмосфері, який не перевищує в середньому t₀c = 660 м. Іншими словами, мюони не могли б досягати поверхні Землі. Насправді ж вони реєструються приладами, встановленими на поверхні Землі, оскільки середній час життя рухомого мюона за годинником земного спостерігача 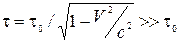і шлях, проходжуваний мюоном за цей час, tV >> 660 м.

Релятивістський ефект сповільнення ходу часу в космічному кораблі, що рухається відносно Землі, відкриває можливість здійснення як завгодно далеких польотів і подорожей “у майбутнє”. Згідно з принципом відносності, всі процеси на космічному кораблі, включаючи і процес старіння космонавтів, ідуть за тими ж законами, що й на Землі. Але при цьому час на кораблі треба вимірювати за годинником, який рухається разом із ним зі швидкістю V відносно Землі. Якщо V близька до с, то годинник на кораблі йде значно повільніше, ніж земний (на космодромі) – в 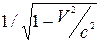разів. Наприклад, при b = V/c = 0,99999 хід годинника на кораблі і на Землі відрізняється в 224 рази. Отже, на такому кораблі за проміжок часу t₀= 10 років за корабельним годинником можна здійснити, постарівши всього лише на 10 років, космічний політ, який за годинником на Землі триватиме t= 2240 років! При цьому корабель віддалиться від Землі на величезну відстань l = Vt = b ct= 2239,98 світлових років (світловим роком називається відстань, яку проходить світло у вакуумі за рік: 1 св.рік = 9,4605(1015 м). Чим ближче V до с, тим більший шлях l може пройти корабель відносно Землі за один і той же проміжок t₀ власного часу на кораблі, тобто тим більш далекий космічний переліт можуть здійснити космонавти за своє життя.

Якщо космонавт, здійснивши космічний політ зі швидкістю V, близькою до с, повернеться на Землю, то він виявить, що люди на Землі (зокрема, його брат-близнюк, який залишився на Землі) постаріли за час польоту більше, ніж він. При достатньо малій відмінності V від с, коли (1 – V ²/c²) >> 1, космонавт може пережити всіх своїх сучасників на Землі і опинитися після повернення серед представників наступних поколінь людей.

На перший погляд здається, що, виходячи з принципу відносності, можна прийти до висновків, прямо протилежних до наведених у п.6: годинник на Землі, яка рухається зі швидкістю – V відносно космічного корабля, повинен відставати від годинника на кораблі. Тому тривалість польоту повинна бути більшою для космонавта, а не для мешканців Землі. Відповідно, за час польоту повинен більше постаріти той із двох близнюків, котрий летів на кораблі.

Таким чином, виходить, що різниця показів годинника на космодромі і на кораблі після приземлення повинна бути, з одного боку, додатною, а з другого – від’ємною. Цей абсурдний результат одержав назву парадоксу годинників, або парадоксу часу. Насправді ніякого парадоксу немає. Він виник унаслідок неправильного застосування принципу відносності. Цей принцип говорить про повну рівноправність не будь-яких систем відліку, а лише інерційних. Між тим, система відліку, пов’язана із космічним кораблем, – на відміну від Земного – не весь час є інерційним, оскільки під час набору швидкості на старті, обльоту цілі і гальмування при спуску корабель рухається з прискоренням. Тому задача про хід годинника на космодромі, який весь час перебуває в спокої відносно однієї й тієї ж інерційної системи відліку, і годинника, який знаходиться на космічному кораблі, принципово несиметрична, а Земна і корабельна системи відліку – нерівноправні в даній задачі. Правильними є міркування, викладені в п.6, оскільки вони засновані на використанні інерційної (Земної) системи відліку. Відповідно міркування на початку п.7, що призвели до парадоксу годинника, – помилкові. У другому випадку слід користуватися не спеціальною, а загальною теорією відносності. При цьому виявляється, що і з точки зору космонавта його годинник повинен іти повільніше, ніж на космодромі.

Інтервалом, або просторово-часовим інтервалом, між двома подіями, виміряним в інерційній системі відліку К`, називається величина

,

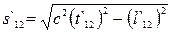де t`<sub>12</sub> = t`₂ + t`₁ – проміжок часу між розглядуваними подіями (за годинником у системі відліку К¢), а 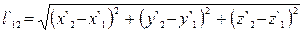– відстань між точками, в яких відбуваються події 1 і 2, виміряна також в системі відліку К¢.

Із перетворень Лоренца випливає, що інтервал між даними двома подіями 1 і 2 інваріантний відносно вибору інерційної системи відліку, тобто не змінюється при переході від рухомої інерційної системи відліку К¢ до нерухомої К:

s`₁₂ = s₁₂ = inv, де .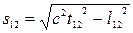

Якщо 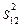>0, тобто s₁₂ – дійсне число, то інтервал s₁₂ називається часоподібним інтервалом.

Інтервал s₁₂ називається просторовоподібним інтервалом, якщо 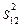<0, тобто s₁₂ – уявне число.

Із інваріантності інтервалу відносно вибору інерційної системи відліку К¢ випливає, що в усіх системах відліку К¢ значення t`<sub>12</sub> і l`₁₂ для даних двох подій 1 і 2 задовольняють рівняння гіперболи:

.

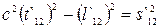Якщо 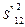>0, то зв¢язок між t`<sub>12</sub> і l`₁₂ у різних інерційних системах відліку К¢, які рухаються відносно нерухомої системи відліку К з усіма можливими швидкостями (0£V<c), зображується графічно у вигляді двох гілок гіперболи І і ІІ (рис. 5.3). Отже, знак проміжку часу між подіями 1 і 2, пов¢язаними часоподібним інтервалом, абсолютний. Він не залежить від вибору інерційної системи відліку: в усіх системах відліку К¢ друга подія відбувається або завжди пізніше першої, тобто t`<sub>12</sub> > 0 (гілка І), або завжди раніше першої, тобто t`₁₂ < 0 (гілка ІІ). Відстань l`<sub>12</sub> відносна, причому можна вказати таку інерційну систему відліку К¢, в якій l`₁₂ = 0, тобто події 1 і 2 відбуваються в одному й тому ж місці (точки А і В на гілках гіперболи І і ІІ).

Двом подіям, пов’язаним причинно-наслідковим зв’язком, завжди повинен відповідати часоподібний інтервал або, в крайньому випадку, нульовий інтервал (s₁₂ = 0). Це зумовлено тим, що сигнал, за допомогою якого подія 1 (причина) спричиняє появу події 2 (наслідок), не може поширюватися в просторі зі швидкістю понад швидкість світла у вакуумі: l`<sub>12</sub> £ c(t`₂ – t`₁).

У випадку подій, пов’язаних просторовоподібним інтервалом (s`<sub>12</sub> < 0), знак t`₁₂ відносний: t`<sub>12</sub> > 0 (верхня частина гіперболи ІІІ на рис. 5.3) в одних інерційних системах відліку К¢, а в інших t`₁₂ < 0 (нижня частина гіперболи ІІІ). Точка С відповідає системі відліку К¢, в якій t`₁₂ = 0, тобто події 1 і 2 відбуваються одночасно.