Z - перетворення дискретного сигналу

Дискретний сигнал і його спектр описуються формулами:

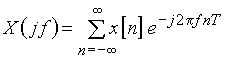; (9.1)

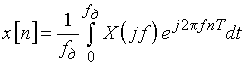. (9.2)

Проведемо у формулі (9.1) заміну: .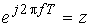

Тоді формула прийме вигляд:

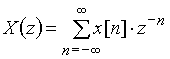. (9.3)

Вираз (9.33) одержав назву z-претворення або z-зображення дискретного сигналу x[n]. Якщо почати підсумовування з n = 0, той вираз

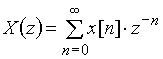. (9.4)

є одностороннє z-претворення. Воно застосовується для сигналів x[n]=0 при n<0.

Можна вказати на зв'язок z-претворення з перетворення Лапласа дискретного сигналу

,

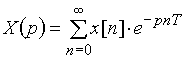яке легке одержати з (9.1), поклавши j2pf = p.

Очевидно, що z = e^рT або p = T^-1ln z.

Ці формули встановлюють зв'язок між точками в площинах p=a+jw_i, z = x+jy (рис. 9.17.).

Якщо покласти а = 0, то ми переміщатимемося по осі jw в площині р. При переході в z-площину точки уявної осі jw розташовуватимуться на одиничному колі z = e^jwT. Причому, точка j0 на р-площині переходить в точку z = +1 на речовинній осі z-площини, а точки ±j0,5w_д – у точку z = –1. Це означає, що точки відрізка (-j0,5w_д ÷ j0,5w_д) р-площини проектуються в точки на одиничному колі z-площини.

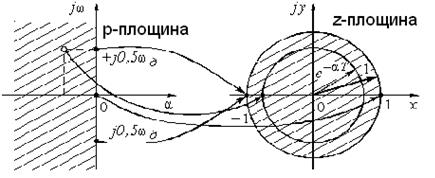
Рис. 9.17. Перенесення точок з p-площини в z-площину.

Оскільки функція 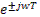періодична, то подальші відрізки осі jw на р-площині такої ж довжини знов проектуватимуться на одиничне коло.

Точкам лівої р-півплощини відповідають крапки усередині одиничного кола z-площини, а точкам правої p-полуплощини – крапки зовні цього кола.

Як знайти дискретний сигнал по його z-претворенню.

Можна скористатися зворотним z-претворенням (подібно тому як ми користуємося зворотним перетворенням Лапласа):

,

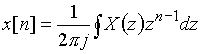де інтеграція ведеться по замкнутому контуру в z-площини.

Інший спосіб полягає в тому, щоб розкласти функцію X(z) у статичний ряд за ступенями z-1. Тоді коефіцієнти при ступенях z-1 будуть, відповідно до формули (9.2), відліків дискретного сигналу x[n].

Дискретний ланцюг може здійснювати будь-які операції: фільтрацію сигналу, коректування характеристик і т.п., тобто виконувати функції будь-якого аналогового ланцюга.

Зокрема, при синтезі дискретних частотних фільтрів потрібно знайти такі коефіцієнти передавальної функції, частотна характеристика якої відповідала б нормам ослаблення фільтру в смугах пропускання і не пропускання (рис. 9.18). Визначення коефіцієнтів – це задача апроксимації. Відомий цілий ряд методів її рішення. Найпоширенішим є наступний метод. Спочатку розраховують аналоговий НЧ-прототип і одержують його передавальну функцію H(p), потім шляхом заміни комплексної змінної p=Ф{z} переходять від H(p) до передавальної функції дискретного ланцюга H(z).

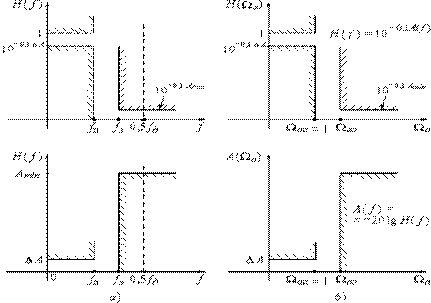
Рис 9.18. Частотні характеристики фільтрів.

Використовування стандартного перетворення z=e pT або p=(1/T)lnz не приведе до дробово-раціональної функції. Тому для ФНЧ застосовують білінійне перетворення

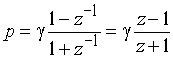. (9.5)

(g – деякий постійний множник), яке є першим наближенням стандартного перетворення при розкладанні його в ряд Тейлора:

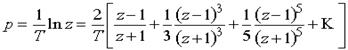. (9.6)

З розкладання (9.5) виходить, що необхідно вибирати g = 2/T. Проте, далі ми покажемо, що зручніше брати інші значення коефіцієнта g .

Білінійне перетворення (9.6) переводить всі крапки з лівої напівплощини змінної p в крапки на одиничному колі площини z. Отже, якщо був стійкий аналоговий ланцюг, буде стійкою і дискретна.

У цифровому фільтрі зберігання і обробка чисел (представлених, як ми вже знаємо, в двійковому коді) здійснюється в пристроях (елементах пам'яті, помножувачах, суматорах) з кінцевим числом розрядів. Тому розрахунок цифрового фільтру, крім визначення передавальної функції H(z) фільтру і його структурної схеми (див. вище) включає також розрахунок розрядів АЦП і ЦАП і розрядів резисторів оперативної пам'яті (помножувачів, суматорів).

Крім того, при розрахунку цифрового фільтру передбачають розрахунок масштабних множників, що вводяться в схему для запобігання переповнювання регістрів фільтру, а також перевірку стійкості фільтру.

Одним з найбільш розповсюджених методів переходу від аналогової до цифрової передатної функції є білінійне перетворення, що дозволяє зіставити кожній комплексній крапці s-площини тільки одну визначену крапку комплексної z-площини. Через нелінійне співвідношення між цифровою й аналоговою частотами цей метод дає кращі результати тільки на нижніх частотах, тому він найбільше підходить при проектуванні фільтрів нижніх частот.

Білінійне перетворення визначається в таким чином:

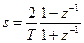(9.7)

де T- період дискретизації сигналів.

Для одержання необхідної функції H(z) цифрового фільтру необхідно зробити заміну:

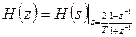(9.8)

Полюси цифрового фільтру можна знайти через полюси відповідного аналогового фільтра за співвідношенням:

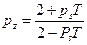(9.9)

З цього вираження видно, що полюси з лівої (стійкої) s-напівплощини відображуються усередині одиничної окружності на z-площині, а полюси з правої (хитливої) s-напівплощини відобразяться на z-площині поза одиничним колом.

Вибір періоду дискретизації завжди впливає на координати полюсів і нулів у комплексної z-площині. Використовуючи рівняння (9.9) можна побудувати графік залежності руху полюсів на площині в залежності від періоду дискретизації T (рис. 9.19).

Рис. 9.19 – Вплив періоду дискретизації T на положення

полюсів у z-площині

При збільшенні періоду дискретизації від 1 до ∞ корені рухаються до точки (-1;0), групуючись навколо неї. Аналогічна ситуація спостерігається при зменшенні періоду дискретизації від 1 до -∞, коли корені рухаються до точки (1;0), групуючись навколо неї. При цьому дійсна частина кореня буде прагнути до -1 чи 1 відповідно, уявна частина буде прагнути до 0.

Ця властивість накладає деякі умови на вибір періоду дискретизації, наприклад, при виборі періоду дискретизації 10^±d точність обчислень при білінійному перетворенні полінома 2-го порядку повинна бути не менш 2d знаків. При білінійному перетворенні поліномів більш високих порядків точність обчислень підвищується в n раз (де n - порядок полінома). Недостатня точність білінійного перетворення може привести до великої похибки і втрати інформації.

Зазначена властивість найбільш актуальна для фільтрів високих порядків n≥10, особливо еліптичних. При підвищенні порядку фільтра найближчі комплексно-сполучені корені розташовуються дуже близько до уявноої осі, тобто дійсна частина прагне до нуля, що у свою чергу підвищує показник коливності.

Якщо при розрахунку цифрового фільтра не можна забезпечити задану точність, то зважується задача вибору компромісного періоду дискретизації.

Таблиця. 9.1. - Форумули заміни для різних типів фільрів.

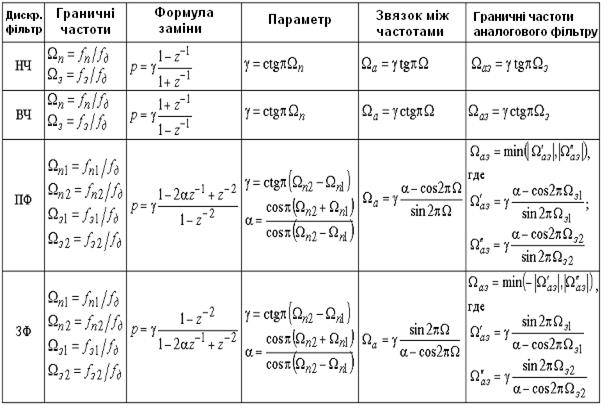
Як випливає з рис. 9.1, період дискретизації варто вибирати так, щоб корені на z - площині знаходилися як найближче до дійсної осі (T≈2), що дозволить значно спростити розрахунок фільтра за рахунок зменшення необхідної точності обчислень.

Якщо позначити період дискретизації фільтра T_ф, а період дискретизації вхідного сигналу Т_вх, то частота зрізу проектованого фільтра буде дорівнювати:

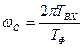. (9.10)

На АЧХ отриманого фільтра одиниці по осі частот потрібно розділити на Т_вх для переходу до дійсних частот. Таким чином, як би розтягується сигнал у часі, а після фільтрації повертається у вихідний стан.

Контрольні запитання

1. Чим є аналогові, дискретні і цифрові сигнли?

2. Як розрахувати z-зображення дискретного сигналу?

3. Що таке радіус збіжності?

4. Яка імпульсна характеристика для нерекурсивних (для рекурсивних) фільтрів: кінцева або нескінченна?

5. Як впливає період дискретизації на динаміку електронних систем ?

6. Що являть собою фільтри із змінною частотою дискретизації ?

7. На які групи ділять способи реалізації цифрових фільтрів ?

8. Навести структурну схему біквадратного НІХ-фільтра.

9. Порівняти КІХ та НІХ фільтри.

10. В чому основна відмінність рекурсивних фільтрів?

11. Чому при реалізації рекурсивних фільтрів обмежується порядок фільтра?

12. Про що свідчить теорема В.А. Котельникова?

13. Як розрахувати z-зображення дискретного сигналу ?

14. Що таке радіус збіжності?