Експоненційне згладжування

Теорія і математичний апарат фільтрів Вінера дозволяє вирішувати задачі синтезу оптимальної структури статистичного фільтра, параметри якого обумовлені характеристиками сигналу, який фільтрується. Результати використання цієї методології доводять, що для необхідного діапазону статистичних характеристик входу фільтр повинен мати інерційно-інтегральні властивості, а його структура — будуватися на підставі інерційних ланок.

Разом з тим, реалізація і практичне використання таких фільтрів наштовхує на деякі труднощі:

· Неперервний варіант фільтра — це спеціальний аналоговий пристрій на кожен з десятків чи сотень інформаційних каналів;

· Дискретний варіант фільтра — повинен мати великий об’єм пам’яті.

Обійти ці труднощі і перевести статистичну фільтрацію на практичні колії можливо шляхом широкого використання засобів обчислювальної техніки і переходу від оптимальних до субоптимальних структур.

При такому переході (рис.11.1.) статистична фільтрація набуває суттєво практичне значення.

Визначимо одну з субоптимальних структур фільтрації для практичного діапазону статистичних характеристик корисного сигналу та некорельованої з ним похибки, приклад 1 для вимірювального каналу:

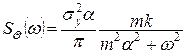; . (11.1)

Вважаючи що Y = 0, переходимо до простішої моделі рис 11.2, яка відповідає прикладу 2 для каналу керування:

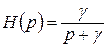, (11.2)

де g = C/T — величина обернено пропорційна постійній часу фільтра при одиничному коефіцієнті передачі.

1. Вимоги. Апостеріорі. Відома структура фільтрів Вінера для практичного діапазоні статистичних характеристик носіїв фільтрації. 2. Аналоговий варіант фільтра з неоптимальними параметрами. 3. Перехід до різницевої форми 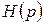-структури. Рекурентний алгоритм з неоптимальними параметрами. 4. Пошук оптимальних параметрів системи за умови досягнення найменшої усталеної похибки: та

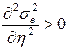
Рис. 11.1. — Процедура переходу до субоптимальної

стохастичної фільтрації.

Рисунок 11.2. — Модель експоненціального згладжування.

Якщо — фільтр володіє диференціальними властивостями.

При — має переважно інтегральні властивості. Так як (11.2) є характеристична форма запису лінійного диференціального рівняння, рішенням якого є функція g=exp(-gt), то вхідний сигнал Z(t), пройшовши через структуру (11.2), отримує експоненційне згладжування. Практичне використання моделі експоненційного згладжування потребує вибору значення єдиного параметра g, виходячи зі статистичних характеристик входу Z(t).

Знайдемо значення g з умови мінімізації похибки фільтрації:

.

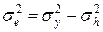Враховуючи у (11.2) , маємо

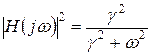; . (11.3)

Тоді:

.

Після перетворень і отримання невласного інтеграла в останньому виразі, отриманого з (11.1) і (11.3), будемо мати:

.

Остаточно можна записати:

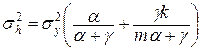; (11.4)

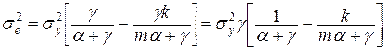. (11.5)

Отримавши похідну і прирівнявши її до нуля, знайшли:

; .

Звідси: 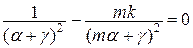або .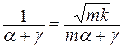

Тоді: 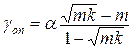, (11.6)

а похибка фільтрації визначається виразом (11.5) при підстановці туди 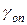з (11.6).

З іншого боку, фільтр експоненційного згладжування буде здійснений у тому випадку, коли g > 0. Це визначає границі використання субоптимального фільтра (11.2) і (11.6)

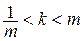. (11.7)

Таким чином, субоптимальний фільтр експоненційного згладжування, як аналоговий пристрій, має структуру (11.2) з єдиним параметром , який знаходимо з (11.6), і робочою областю (11.7), обумовленою параметрами похибки. Зокрема, якщо параметр 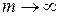, завада зі спектральною щільністю (11.1) трансформується в білий шум:

.

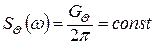В цьому випадку, слідуючи за алгоритмом рис.11.2, маємо:

;

.

З урахуванням цього:

;

,

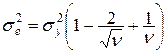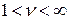де 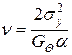— дисперсійне відношення “сигнал/завада”.

На відміну від оптимальної фільтрації, де при відсутності завади , при експоненціальному згладжуванні в цьому випадку 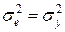, у випадку гранично великої похибки, коли , тоді :

;

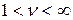. (11.8)

В цьому парадокс експоненціального згладжування білого шуму.

Наявність засобів обчислювальної техніки у контурі контролю потребує формування і практичного використання дискретного аналога експоненціального фільтра. Вихідним для дискретної уяви фільтра служить передаточна функція (11.2):

;

aбо 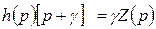. (11.9)

Запровадимо дискретний час 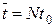, де 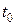— крок квантування, а N=0,1,2,3.... Тоді перехід від неперервного часу t, в якому функціонує фільтр-пристрій, до дискретного або 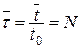еквівалентний переходу від звичайного перетворення Лапласа до дискретного (D–перетворення). У просторі зображень цьому відповідає перехід від алгебраїчних рівнянь типу (11.9) до різницевих, тобто операція множення на змінну р замінюється різницею 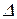, а множення на — додаванням .

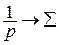
Тоді з (11.9) отримали: ,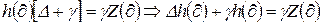

або в оригіналі:

, (11.10)

де .

Звідти: .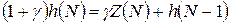

Остаточно: 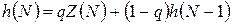, (11.10)

де ; .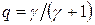

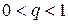У підсумку, (11.10) — є рекурентний алгоритм експоненціальної фільтрації, що працює у дискретному часі з інтервалом опитування датчика t₀. Цей фільтр-алгоритм визначає шукане значення вимірюваної змінної на виході фільтра h(N) у поточний момент 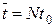через вимірюване значення змінної у цей самий момент і значення виходу h(N-1) у момент попереднього опитування (N-1) t₀. Безсумнівною перевагою цього алгоритму є те, що його реалізація на ЕОМ потребує лише однієї комірки пам’яті незалежно від величини інтервалу t₀. Однак, зменшення об’єму пам’яті, необхідної для здійснення алгоритму (11.10) в ЕОМ, призводить до того, що похибка фільтрації стає залежною від двох параметрів і t₀.

Для того щоб дискретний експоненціальній фільтр (11.10) став субоптимальним, необхідно вирішити задачу про мінімум похибки фільтрації і в цьому випадку. Виходячи з (11.10) як рекурентного співвідношення для різних моментів дискретного часу: 0; t₀; 2t₀; 3t₀;…N*t₀, отримаємо:

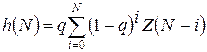. (11.12)

В стаціонарному режимі вимірювання похибка фільтрації становить:

. (11.13)

Підставимо у (11.13) значення h(N) з (11.12) та використовуючи (11.1) отримаємо:

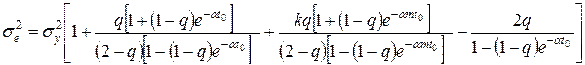(11.14)

Так як: 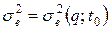, то тут можливо два випадки:

1) При t₀=const, знайдемо значення q (або g, що теж саме) з умови мінімуму похибки:

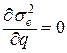; ; (11.15)

2) При q=const, знайдемо значення t₀ з тієї ж умови

; .

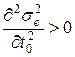Перший випадок є найліпшим для практичного використання рекурентного алгоритму (11.10). Він дозволяє для встановленого раніше періоду опитування датчиків 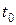, котрий обумовлений багатьма факторами функціонування вимірювальних систем, зробити експоненціальну фільтрацію субоптимальною. Разом з тим, оптимальне значення 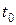, визначеного у другому випадку, наштовхується на серйозні труднощі, так як в більшості випадків потребує надзвичайно високої швидкості опитування датчиків, що технічно забезпечується далеко не завжди. В такому випадку спробуємо вирішити задачу за пунктом 1, для чого візьмемо похідну від виразу (11.14) та прирівняємо її до нуля. При цій умові після перетворень отримаємо:

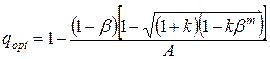, (11.16),

де 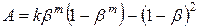і .

Вираз (11.16) діє, якщо 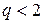, в противному випадку ряд (11.12) розходиться.

Зокрема, якщо 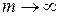, завада A трансформується у білий шум і з (11.16) витікає:

, (11.17)

внаслідок того, що .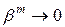

Таким чином, в вимірювальних системах для фільтрації вимірюваної інформації від некорельованих похибок з’являється можливість використання в якості експоненціального фільтра рекурентного алгоритму (11.10), субоптимальність якого забезпечується виразами (11.16) чи (11.17) відповідно до характеру похибки. Границі використання фільтра:

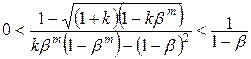; (11.18)

або (11.19)

у випадку білого шуму. У формулах (11.17) та (11.19) параметр k переходить у 1/v, де v визначається дисперсійним віднощенням сигнал-завада.