Резюме.

При виводі виразів (11.46), (11.48), (11.49) використовувалися результати того, що конкретної функції:

,

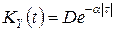що має властивості парності, зсув за часом на величину Δ дає :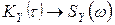

;

,

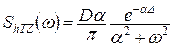що змінює частотну характеристику системи внаслідок отримання нею прогнозуючих властивостей.

,

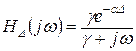а значить змінюється і модуль .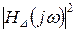

Сама система володіє зсуваючими властивостями.

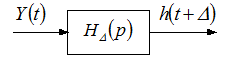
Через це у виразі відносно 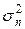сигнал 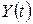входить без зсуву.

Можна поступити інакше:

формально на підставі теорії про зсув оригіналу

,

.

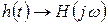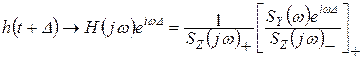Таким чином 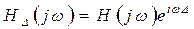, тобто якщо зсунути у часі вхідний сигнал 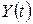, то частотна характеристика системи залишається колишньою:

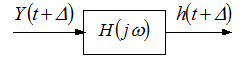
і тоді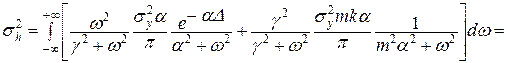

.

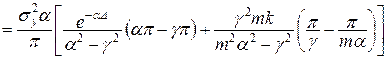або

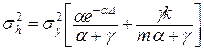. (11.50)

Звідси похибка:

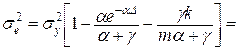
. (11.51)

Мінімізуючи останній вираз по γ, отримаємо:

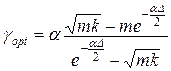, (11.52)

котре як і (11.49), при 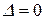дає вираз (11.47).

Контрольні запитання

1. В чому парадокс експоненційного згладження білого шуму?

2. Розкажіть про фільтр Вінера, наведіть його структурну схему.

3. Що таке автокореляційна функція?

4. Назвіть критерії статичної оцінки сигналу.

5. Назвіть засоби аналогової корекції.

6. Навести структуру реального неперервного експоненційного фільтра.

7. Розкажіть про операції фільтрації та інтерполяції.

8. Наведіть структуру системи, що володіє зсуваючими властивостями.

9. Як визначається похибка фільтрації?

10. Наведіть основні рекомендації щодо практичного використання експоненційного і стохастичного фільтрів.

11. Розкажіть етапи процедури переходу до субоптимальної стохастичної фільтрації.

12. Як визачається величина обернено пропорційна постійній часу фільтра при одиничному коефіцієнті передачі?

13. Що необхідно для того, щоб дискретний експоненціальній фільтр став субоптимальним?

14. Наведіть приклади застосування експоненційної і стохастичної фільтрації.