Компенсації збурень

Керування технологічними об'єктами відбувається в умовах неповної інформації, при цьому обмежене число вхідних параметрів регіструється з помилками, крім того неконтрольовані збурення при ідентифікації, які е перешкодами, чинять суттєвий вплив на вихідні параметри, які вимірюється зі значним транспортним запізненням. При роботі в умовах перешкод градієнт функціоналу невідомий, а відомі лише градієнти його реалізацій. З належним вибором матриці підсилення можна користуватися всіма різновидностями регулярних ітеративних алгоритмів, замінивши в них градієнт функціоналу на градієнт його реалізації.

Алгоритм поточного усереднення має наступний вигляд

. (12.22)

Рівняння (12.22) являє собою ітераційну формулу для розрахунку середнього значення У_n/Х_in, якщо .

Розглянемо три модифікації алгоритмів адаптивної ідентифікації, які мають таку ж структуру, як і (12.22), але відрізняються способом подання початкової інформації, тобто формуванням поправки.

Для часткової локалізації впливу неконтрольованих збурень і перешкод і зменшення кількості пошукових рухів системи, особливо при відсутності апріорної інформації, введені обмеження. Алгоритми дозволяють оцінити усередненні оцінки взаємозв'язку контрольованих входів і виходу, а також взаємозв'язок між вхідними збуреннями.

Перша модифікація являє собою метод для озрахунку середнього відхилення вихідного параметру

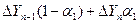, коли 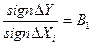(12.23)

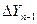, якщо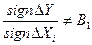

де 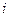- порядковий номер збурення;

- відхилення вихідного параметра на n -му і n-1 кроках;

α₁ - параметр усереднення;

В₁ - апріорно заданий знак залежності 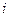-го збурення і вихідного параметру.

Аналогічна процедура може бути використана для аналізу відхилень вхідних збурень. Розглянута процедура відрізняється простотою і доцільна при керуванні одновимірними об'єктами з відносно невисоким рівнем перешкод.

Друга модифікація вміщує, по суті, обчислення оцінок градієнту процесу, використовуючи коефіцієнти парних регресій.

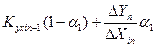, коли DX_in>Q_xi

K_yxin= 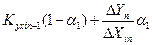, коли DX_in=Q_xi (12.24)

де K_yxin - оцінки коефіцієнтів передачі технологічного процесу між входами Хi і виходом У;

α₁ - параметр алгоритму;

Q_xi - зона нечутливості при вимірюванні збурень;

DX_in=Q_xi - відповідно відхилення поточних виміряних значень збурень Хi і вихідної координати У від поточних середніх.

Обмеження Q_xi в формулах (12.24) дозволяють частково локалізувати вплив неконтрольованих збурень і перешкод N на Kyxin являються, по суті, зоною нечутливості, вибір якої визначається апріорною інформацією про рівень перешкод N.

Введення обмежень Q_xi виключає ділення на нуль у (12.24) і тому, в окремому випадку, можна показати, що відношення 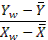, усереднене на п. кроках, являє собою оцінку коефіцієнта парної регресії. Дійсно, оцінку коефіцієнта парної регресії можна представити у вигляді

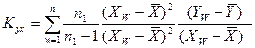. (12.25)

Якщо відношення відхилень У_W і Х_W від поточних середніх представляють собою оцінку коефіцієнта парної регресії К_yx, обчисленого з помилкою , то рівняння приймає вигляд

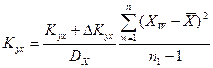(12.26)

При достатньо великих n1, коли співмножник (12.26) представляє оцінку дисперсій D_X, одержимо, що DK_yx=0.

Наведена процедура по формі співпадає з рівнянням (12.24) і рекомендується для визначення керуючих впливів в багатовимірних системах з підвищеним рівнем перешкод. Недолік процедури полягає в тому, що при невеликих відхиленнях збурення і відносно великих за рахунок впливу неконтрольованих збуджень відхиленнях вихідного параметру оцінка шуканого коефіцієнта буде завищеною. 8 значному ступені він усувається введенням обмежень, однак, це приводить до неповного використання початкової інформації.

Третя модифікація дозволяє усунути ділення відхилень вхідного і вихідного параметрів. В цьому випадку усереднена оцінка коефіцієнта передачі процесу визначається в наступному вигляді.

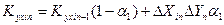(12.27)

де K_yxin-1- оцінка кореляційного моменту між входом і виходом на n-1 крапці.

Початкова інформація представляється у вигляді добутку поточних відхилень входу і виходу DX_in·DY_n. Тоді математичне сподівання добутку являється оцінкою кореляційного моменту.

Застосування добутку DX_in·DY_n замість їх відношення дає безсумнівні переваги в обчислювальному відношенні. Оскільки відношення відхилень збурень і вихідного параметру представляє оцінку коефіцієнта парної регресії, у відповідності з рівнянням (12.27), то можна записати

. (12.28)

де K_yx - коефіцієнт регресії;

D_X - дисперсія вхідного збурення.

Звідки виходить, що усереднений на п. кроках добуток відхилень вхідного збурення і вихідного параметра представляє собою оцінку кореляційного моменту. Застосування вказаної процедури доцільно при визначенні керуючих впливів в багатовимірних системах з відносно високим рівнем неконтрольованих збурень і перешкод.

На вхід контуру адаптації коефіцієнта передачі між керуючим впливом і збуренням поступає корисний сигнал у вигляді добутку (частки) вихідного параметра і збурення, а також перешкода. Вимагання по швидкодії контурів стають суперечними, що дозволено в задачі стохастичного синтезу.

Розглянемо реалізацію отриманих рішень шляхом послідовно­го (паралельного) включення найпростіших динамічних ланок. Для цього розглянемо апроксимацію рекурентних алгоритмів типовими безперервними динамічними ланками.

Комплексний коефіцієнт посилення лінеаризованої цифрової системи практично співпадає з комплексним коефіцієнтом підсилення безперервної системи, якщо найбільший по модулю уявний полюс комплексного коефіцієнта підсилення або найбільше значення уявної частини комплексного кореня значно менше величини, оберненої періоду дискретності. Наприклад, в застосуванні синтезу рекурентних алгоритмів для задач точної прокатки вказані умови виконуються, так як значення резонансної частоти випадкових процесів складають 0,01 - 0,1 Гц, а період дискретності Т > 0,5 с, тоді помилка не перевищує 2 відсотків.

В таблиці 12.1. приведені безперервні динамічні моделі, що апроксимують рекурентні процедури, а також взаємозв'язки постійних часу типових динамічних ланок з параметрами рекурентних процедур. Оскільки в рекурентних процедурах застосовується поточна інформація, то для отримання моделей передаточних функцій входом вважаємо добуток двох функцій, а виходом - оцінку шуканого коефіцієнта передачі.

Процедура №і Роббінса Монро (рядок і, табл. 12.1.) характеризується збільшенням (зменшенням) оцінки коефіцієнта на фіксовану величину пропорційно величині оцінки добутку функцій і вагового коефіцієнта. Еквівалентна динамічна ланка асимптотичне зводиться до інтегруючої.

Рішення різницевих рівнянь (12.9), (12.10), (13.12), що використовується для усереднення шляхом ділення суми виміряних значень параметра на кількість вимірювань, зводяться до наступного виразу

æ æ)^w (12.28)

Справа у формулі (12.28) стоїть згортка вхідного сигналу.

Таблиця 12.1. - Апроксимація рекурентних процедур типовими динамічними ланками

№	Рекурентні алгоритми	Еквіва-лентні динамічні ланки	Значення параметрів, с
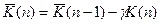
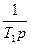
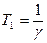
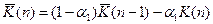
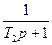
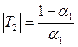
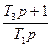
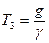
Продовження таблиці 12.1

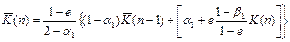
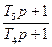
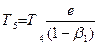
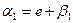
Y_n-w / X_n-w і вагової функції w=(1 - æ)^w. Така вагова функція відповідає інерційній ланці першого порядку. В приведених формулах при підсумовуванні значення випадкових величин Y_n-w / X_n-w беруться з вагою, яка убуває за геометричною прогресією в минуле.

Для стаціонарних і ергодичних процесів математичне очікування оцінки середнього значення Y_n-w / X_n-w, обчислене по формулі (12.24) співпадає при великих п з математичним сподіванням М(Y_n-w / X_n-w) і випадкова величина трансформується в невипадкову. При кінцевих n оцінка одержується дещо заниженою за абсолютною величиною.

Процедура №2 (рядок 2, табл. 12.1.) апроксимується асимптотичним еквівалентною аперіодичною ланкою першого порядку. Так для усереднення випадкових функцій використовують формулу для поточного середнього, до якої зводиться розглянута процедура при а=і/n. В цьому випадку постійна часу аперіодичної ланки залежить від параметра, що визначає питому вагу уточнення моделі, а процедура еквівалентна алгоритму Качмажу. Розглянута модель може бути отримана на основі приведеної процедури №і шляхом охоплення жорстким від'ємним зворотним зв'язком відпо­відної їй динамічної ланки.

Рекурентні алгоритми 3 і 4 синтезовані на основі перших двох, де в прямому каналі перетворення інформація розділяється на суму пропорційної і інтегральної складових.

В процедурі №3 (рядок 3, табл. 12.1) g - відносна величина пропорційної складової помилки. В процедурі №4 величини пропорційної і інтегральної складових дорівнюють е і β, причому a₁=e+b.

Арсенал типових рекурентних алгоритмів, приведених у табл. 12.1., може бути розширений шляхом використання від'ємних зворотних зв'язків. В табл. 12.2. приведені безперервні динамічні моделі раніш розглянутих рекурентних алгоритмів, що вміщують одиничні від'ємні зворотні зв'язки. Розглянуті моделі, які не мають транспортного запізнення, а також моделі з запізненням, рівним одному виміру.

Аналіз моделей показав, що реалізація оптимальних рішень у задачах ідентифікації і керування в більшості випадків можлива лише при відсутності запізнення.

Розглянуті особливості задач ідентифікації і керування. При вирішенні задач ідентифікації технологічного процесу необхідно забезпечити реалізацію типовими динамічними ланками оптимальної передаточної функції. При цьому розглядається оптимальна передавальна функція замкненої системи. Наприклад, для реалізації аперіодичної ланки першого порядку досить використати базовий алгоритм або його модифікацію. Таким чином, відомий алгоритм дозволяє вирішити задачу ідентифікації. Отримана модель може бути вихідною для вирішення наступної задачі - керування технологічним процесом. Для цього потрібно використати додаткову ітераційну процедуру уточнення керування. В відомому алгоритмі така процедура не передбачена. Чим ближче оцінка вектора шуканих коефіцієнтів до дійсного значення, тим більше відносний вплив перешкод. Зокрема, при досягненні оцінкою дійсного значення вплив перешкод приводить до непотрібного (і невірного) уточнення моделі. Зменшення ваги поправки прин­ципово не усуває цей недолік і приводить до суттєвого уповільнення процесу настроювання. Тому в регуляторі, який при керуванні об'єктом прагне забезпечити інваріантність системи по відношенню до контрольованих вхідних збурень, відбувається

Таблиця 12.2. Еквівалентні смуги пропускання білого шуму

№	Передаточні функції систем	Еквівалентні смуги
Розімкнутих	Замкнутих	Смуга пропускання, Гц	Постійна часу, с
			-	-
				-

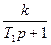
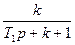
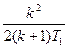
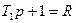
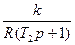
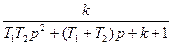
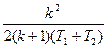
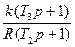
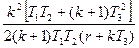
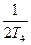
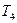
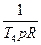
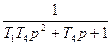
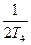
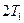
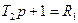
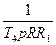
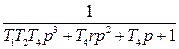
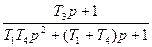
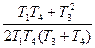
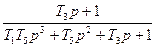
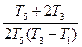
Відносне збільшення рівня перешкод погіршує роботу ідентифікатора. Процес ідентифікації тут уповільнюється і в деяких випадках може розходитись.

Задача керування відрізняється тим, що керуючий вплив замикає динамічну систему аналогічно одиничному від'ємному зворотному зв'язку. Тому для синтезу оптимальних динамічних керованих систем доцільно розглядати реалізацію передаточних функцій розімкнутих систем.

Аналіз передаточних функцій розімкнутих систем показує, що модель уточнення коефіцієнтів керуючих впливів повинна включати процедури 1 і 3 (табл. 12.1.). Використання, наприклад, процедури 2 недоцільно, оскільки замикання одиничного від'ємного зворотного зв'язку при керуванні значно знижує коефіцієнт передачі у замкнутій системі і статична помилка досягає 50 відсотків.

При вирішенні практичних задач ідентифікації і керування інформацію про вихідний параметр отримують з деяким запізненням. При зсуві інформації на один крок безперервні моделі ітераційних процедур зводяться до немінімально - фазових динамічних ланок, які мають нуль в правій на півплощині параметра Р. Тоді транспортне запізнення в системі регулювання не дозволяє реалізувати оптимальні моделі. Отримані в задачі ідентифікації квазіоптимальні рішення по характеристичним рівнянням співпадають з оптимальними тільки для моделей без одиничних від'ємних зворотних зв'язків. Наприклад, відома процедура Качмажу (рядок 2, табл. 12.1.) має безперервний аналог у вигляді немінімально - фазової ланки першого порядку. Для забезпечення стійкості системи необхідно виконати умову T₂-k/(k+1)≥0, що можливо при a₁(k+1)≤1, а при К=1 a₁≤0,5, причому усталена помилка досягає 50 відсотків. Значення коефіцієнта передачі розімкнутої системи на кожному кроці ітерації відрізняється від асимптотичного значення, що може ще в більшому ступені збільшити помилку, так при К=9 a₁≤0,1. Цим можна пояснити відомий факт, що в замкнутій системі керування можливий нестійкий режим настроювання. Забезпечення стійкості не забезпечує оптимальної траєкторії настроювання, що мінімізує середні втрати. Кроковий зсув інформації не дозволяє забезпечити оптимізацію з мінімально можливою помилкою.

Розглянемо вплив параметрів передаточної функції на смугу пропускання системи і еквівалентну постійну часу. ітераційні процедури мають якість згладжування впливу збуджень. Інтенсив­ність фільтрації може бути визначена по величині еквівалентної смуги пропускання. Для цього визначили дисперсію коефіцієнта передачі, рахуючи, що вхідним сигналом являється спектральна щільність білого шуму, оскільки смуга пропускання частот ітераційних процедур значно менше спектра збурень, а тому інтенсивність сигналу рахується постійною. Тоді

. (12.29)

де w₃(iw) - амплітудно-частотна характеристика замкненої системи;

Dw - еквівалентна смуга пропускання білого шуму.

В таблиці 12.2. приведені смуги пропускання динамічних систем. Аналіз результатів показує, що функції 1-3 мають статичну помилку у визначенні коефіцієнта передач, тим більше, чим менше коефіцієнт передачі. Функції 4 - 9 в цьому відношенні краще.

Введення в згладжувальні пристрої додаткових постійних часу, тобто підвищення їх порядку, не являється бажаним, так як це розширює смугу пропускання і погіршує згладжування. Сукупність алгоритмів з передаточною функцією 6 табл. 13.2. гірше згладжує перешкоду типу білого шуму, ніж алгоритм 5, а процедура 9 гірше, ніж 8. У випадку використання процедур 4 і 5 смуги пропускання однакові. 8 цьому випадку додаткова фільтрація, яка вноситься постійною часу, компенсується підвищенням коливальності системи. 8 усіх інших випадках підвищення коливальності являється більш суттєвим, ніж додаткова фільтрація, що вноси­ться введенням нової сповільнюючої постійної часу. Тому вве­дення додаткових постійних часу погіршує згладжування.

Порівняння смуг пропускання оптимальних рішень 7 і 8 показує, що кращими фільтруючими здібностями володіє функція 7, яка також краще, ніж функція 4, однак це проявляється тим си­льніше, чим більше 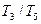. При малих значеннях перевагу слід віддати процедурі з передаточною функцією 4. Швидкодію ітераційних процедур, апроксимованих динамічними ланками першого порядку, можна оцінити по величині постійної часу, а для ланок другого порядку по еквівалентній постійній часу, що дорівнює оберненому значенню коефіцієнта затухання ланки.

Крива перехідного процесу є асимптотичним настроюванням шуканого коефіцієнта передачі, її можна отримати аналітичним шляхом. Оцінка часу перехідного процесу дозволяє оцінити кількість необхідних ітерацій, коли значення коефіцієнта відрізняється від фактичного на величину заданої помилки.

З врахуванням формул (12.12) для визначення часу, при якому має місце максимум перехідної функції, і (12.13) для визначення параметра затухання знаходимо відношення часів досягнення максимуму перехідної функції і першого мінімуму автокореляційної функції у вигляді

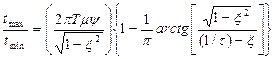(12.30)

Наприклад, для одиничного ступеня регулярності диференційованого випадкового процесу і відношенні дисперсій процесу до перешкоди рівнім нулю у відповідності з формулами (12.12); (12.13) і (12.14) знаходимо, що в форсованій системі Т_μ=0,7; ξ=0,707; τ=0,7, а шукане відношення дорівнює t_max/t_min=1,5p

Таким чином, час досягнення максимума перехідної функції настроювання шуканого коефіцієнта передачі пропорційний часу досягнення мінімума автокореляційної функції процесу.

На основі формули (12.30) для визначення моменту часу, при якому перехідна функція визначення коефіцієнта передачі має помилку регулювання, що не перевищує А, з врахуванням формули (12.30) для визначення параметра затухання випадкової функції процесу, знайшли відношення часів регулювання в форсованій системі з заданою помилкою і досягнення першого мінімума автокореляційної функції у вигляді

. (12.31)

де D - помилка регулювання;

t_Λ - час досягнення заданого значення, коли помилка не перевищує допустимого значення;

t - відношення постійних часу завадостійкої системи;

t_min- час досягнення першого мінімуму автокореляційної функції;

Відносний час визначення асимптотичного настроювання коефіцієнта передачі тим менше, чим більше відношення дисперсій процесу і перешкоди і менше амплітуда відносного відхилення А1, що визначається формулою (12.31).