Основний закон динаміки обертального руху
4.3.1. Розглянемо рух матеріальної точки маси 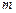 під дією сили
під дією сили 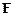 . Нехай точка має імпульс
. Нехай точка має імпульс 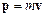 . Радіус-вектор точки позначимо
. Радіус-вектор точки позначимо  . Із закона Ньютона випливає, що
. Із закона Ньютона випливає, що 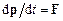 . Домножимо це рівняння векторно на вектор
. Домножимо це рівняння векторно на вектор  . Отримаємо
. Отримаємо
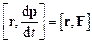 ,
, 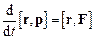 ,
,
або, з урахуванням означень моментів імпульсу і сили,
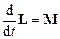 .
.
Останнє рівняння має назву рівняння моментів, воно є найголовнішим рівнянням у динаміці обертального руху матеріальної точки.
Особливо простий вигляд приймає рівняння моментів у випадку, коли матеріальна точка рухається по колу, тобто коли радіус-вектор не змінює своєї довжини і дорівнює радіусу обертання. Візьмемо означення 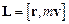 і підставимо в нього відомий вираз з кінематики обертального руху
і підставимо в нього відомий вираз з кінематики обертального руху  . Отримаємо
. Отримаємо 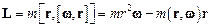 . У цьому виразі другий доданок дорівнює нулю, оскільки скалярний добуток взаємно перпендикулярних векторів
. У цьому виразі другий доданок дорівнює нулю, оскільки скалярний добуток взаємно перпендикулярних векторів 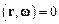 . Отже
. Отже 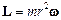 , або
, або
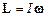 ,
,
де 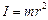 - момент інерції точки відносно розглядуваної осі обертання.Тоді рівняння моментів набуває вигляду
- момент інерції точки відносно розглядуваної осі обертання.Тоді рівняння моментів набуває вигляду
 ,
,
де  - кутове прискорення.
- кутове прискорення.
4.3.2. Тепер розглянемо рух системи матеріальних точок. Запишемо закон Ньютона (рівняння руху) для кожної з n точок системи
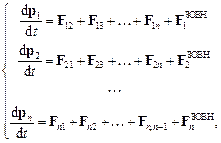
де 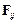 - внутрішні сили. Кожне з отриманих рівнянь домножимо векторно на відповідний радіус-вектор точки
- внутрішні сили. Кожне з отриманих рівнянь домножимо векторно на відповідний радіус-вектор точки  і додамо ліві і праві частини системи рівнянь. При цьому доданки, що містять внутрішні сили, взаємно скоротяться, і ми отримаємо, що перша похідна за часом t від моменту імпульсу
і додамо ліві і праві частини системи рівнянь. При цьому доданки, що містять внутрішні сили, взаємно скоротяться, і ми отримаємо, що перша похідна за часом t від моменту імпульсу 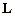 механічної системи відносно будь-якої нерухомої точки О дорівнює головному моментові
механічної системи відносно будь-якої нерухомої точки О дорівнює головному моментові 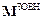 відносно тієї ж точки О всіх зовнішніх сил, прикладених до системи:
відносно тієї ж точки О всіх зовнішніх сил, прикладених до системи:
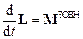 .
.
Отримане рівняння – рівняння моментів - виражає закон зміни моменту імпульсу механічної системи. Як бачимо, рівняння моментів для системи точок виглядає аналогічно рівнянню моментів для однієї точки. Воно справедливе також для твердого тіла, яке шарнірно закріплене в точці О і обертається навколо неї. У такому випадку це рівняння виражає основний закон динаміки твердого тіла, що обертається навколо нерухомої точки.
У проекціях на осі нерухомої прямокутної декартової системи координат із початком у точці О закон зміни моменту імпульсу системи записується у вигляді:
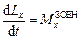 ,
, 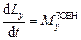 ,
, 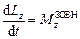 .
.
Тут 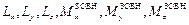 – моменти імпульсу системи і головні моменти зовнішніх сил відносно відповідних осей координат.
– моменти імпульсу системи і головні моменти зовнішніх сил відносно відповідних осей координат.
Якщо тверде тіло обертається навколо нерухомої осі OZ з кутовою швидкістю 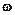 , то його момент імпульсу відносно цієї осі
, то його момент імпульсу відносно цієї осі
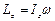 і
і 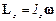 .
.
Тут 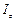 – момент інерції тіла відносно осі OZ, який не змінюється з часом. Основний закон динаміки (силоруху) твердого тіла, яке обертається навколо нерухомої осі OZ:
– момент інерції тіла відносно осі OZ, який не змінюється з часом. Основний закон динаміки (силоруху) твердого тіла, яке обертається навколо нерухомої осі OZ:
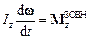 або
або 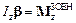 .
.
Із останньої формули видно, що момент інерції твердого тіла відносно якоїсь нерухомої осі є мірою інертності цього тіла в обертанні навколо цієї осі: чим більший момент інерції тіла, тим меншого кутового прискорення воно набуває під дією одного й того ж моменту зовнішніх сил.
4.3.3. Коли матеріальна точка обертається навколо осі з кутовою швидкістю 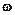 , вона має кінетичну енергію, яку можна розрахувати як
, вона має кінетичну енергію, яку можна розрахувати як
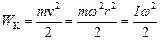 .
.
Аналогічно, кінетична енергія твердого тіла, що обертається навколо нерухомої осі OZ з кутовою швидкістю 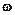 ,
,
 .
.
Кінетична енергія твердого тіла, яке обертається навколо нерухомої точки з кутовою швидкістю 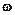 :
:
 ,
,
де I – момент інерції тіла відносно миттєвої осі обертання.
4.3.4. Елементарна робота, виконувана за малий проміжок часу 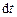 силою
силою 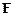 , прикладеною до тіла, яке обертається навколо фіксованої осі, дорівнює
, прикладеною до тіла, яке обертається навколо фіксованої осі, дорівнює
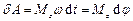 ,
,
де 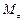 – момент сили
– момент сили 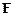 відносно осі обертання OZ (орт осі OZ збігається за напрямком з вектором
відносно осі обертання OZ (орт осі OZ збігається за напрямком з вектором 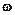 ).
).
Приріст кінетичної енергії твердого тіла за час 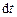 дорівнює роботі зовнішніх сил:
дорівнює роботі зовнішніх сил:
 ,
,
де 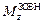 – головний момент зовнішніх сил відносно осі обертання тіла.
– головний момент зовнішніх сил відносно осі обертання тіла.
4.3.5. Елементарна робота, виконувана за малий проміжок часу 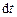 силою
силою 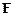 , яка діє на тіло, дорівнює
, яка діє на тіло, дорівнює
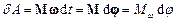 ,
,
де 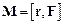 – момент сили
– момент сили 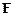 відносно точки О (
відносно точки О (  – радіус-вектор, проведений із О в точку прикладання сили
– радіус-вектор, проведений із О в точку прикладання сили 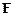 ),
), 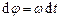 і
і 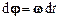 – відповідно кут повороту і вектор елементарного повороту тіла за час
– відповідно кут повороту і вектор елементарного повороту тіла за час 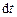 , а
, а  – момент сили
– момент сили 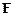 відносно миттєвої осі обертання тіла, рівний проекції вектора
відносно миттєвої осі обертання тіла, рівний проекції вектора 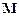 на напрямок вектора
на напрямок вектора 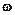 .
.
Приріст кінетичної енергії твердого тіла за час dt дорівнює роботі зовнішніх сил:
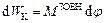 ,
,
де  – головний момент зовнішніх сил відносно миттєвої осі обертання тіла.
– головний момент зовнішніх сил відносно миттєвої осі обертання тіла.
4.3.6. Таким чином, рух вільного твердого тіла задовольняє такі два диференціальні (відоймові) рівняння:
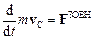 ,
,
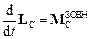 .
.
Тут 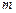 – маса тіла,
– маса тіла,  – швидкість його центра інерції С,
– швидкість його центра інерції С, 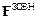 – головний вектор зовнішніх сил, прикладених до тіла,
– головний вектор зовнішніх сил, прикладених до тіла, 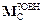 – головний момент зовнішніх відносно точки С сил, а
– головний момент зовнішніх відносно точки С сил, а 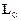 – момент імпульсу тіла відносно тієї ж точки С. Перше рівняння описує поступальний рух вільного тіла зі швидкістю його центра інерції. Друге рівняння випливає з закону зміни моменту імпульсу і описує обертання твердого тіла навколо його центра інерції.
– момент імпульсу тіла відносно тієї ж точки С. Перше рівняння описує поступальний рух вільного тіла зі швидкістю його центра інерції. Друге рівняння випливає з закону зміни моменту імпульсу і описує обертання твердого тіла навколо його центра інерції.
Кінетична енергія вільного тіла може бути знайдена на основі теореми Кеніга:
 ,
,
де 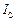 – момент інерції тіла відносно миттєвої осі обертання, яка проходить через його центр інерції С,
– момент інерції тіла відносно миттєвої осі обертання, яка проходить через його центр інерції С, 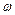 – кутова швидкість тіла. У загальному випадку миттєва вісь переміщується в тілі і момент інерції
– кутова швидкість тіла. У загальному випадку миттєва вісь переміщується в тілі і момент інерції 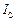 змінюється з часом. Величина
змінюється з часом. Величина 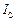 залишається сталою, якщо рух тіла є плоским.
залишається сталою, якщо рух тіла є плоским.
 Приклад. Кінетична енергія однорідного кругового циліндра, який скочується з похилої площини без просковзування. Рух циліндра – плоский: усі його точки рухаються в паралельних (сулежних) вертикальних площинах. Циліндр рухається поступально зі швидкістю
Приклад. Кінетична енергія однорідного кругового циліндра, який скочується з похилої площини без просковзування. Рух циліндра – плоский: усі його точки рухаються в паралельних (сулежних) вертикальних площинах. Циліндр рухається поступально зі швидкістю  , спрямованою вздовж похилої площини, і обертається навколо своєї осі (
, спрямованою вздовж похилої площини, і обертається навколо своєї осі ( 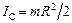 , де
, де 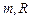 – відповідно маса та радіус циліндра) з кутовою швидкістю
– відповідно маса та радіус циліндра) з кутовою швидкістю 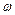 . Із умови відсутності просковзування випливає, що миттєві швидкості точок торкання циліндра об похилу площину дорівнюють нулеві, тобто
. Із умови відсутності просковзування випливає, що миттєві швидкості точок торкання циліндра об похилу площину дорівнюють нулеві, тобто 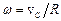 . Тому кінетична енергія скочуваного циліндра
. Тому кінетична енергія скочуваного циліндра
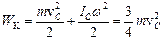 .
.
Дата добавления: 2015-04-07; просмотров: 4208;
