Момент сили і момент імпульсу
Для характеристики зовнішньої механічної дії, яка призводить до зміни обертального руху тіла, вводять поняття моменту сили. Слід розрізняти момент сили відносно нерухомої точки і відносно нерухомої осі.
Моментом сили відносно нерухомої точки О (полюса) називається векторна величина 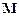 , що дорівнює векторному добуткові радіуса-вектора
, що дорівнює векторному добуткові радіуса-вектора  , проведеного з точки О в точку А прикладання сили (рис. 4.1), на вектор сили
, проведеного з точки О в точку А прикладання сили (рис. 4.1), на вектор сили 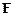 :
:
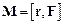 .
.
 Вектор моменту сили перпендикулярний площині, в якій знаходяться радіус-вектор і вектор сили. Модуль моменту сили
Вектор моменту сили перпендикулярний площині, в якій знаходяться радіус-вектор і вектор сили. Модуль моменту сили 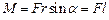 , де
, де 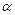 – кут між векторами
– кут між векторами  і
і 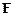 , а
, а  – довжина перпендикуляра ОВ (рис. 4.1), який проведено з точки О до лінії дії сили. Величина l називається плечем сили відносно точки О. При перенесенні точки прикладання сили
– довжина перпендикуляра ОВ (рис. 4.1), який проведено з точки О до лінії дії сили. Величина l називається плечем сили відносно точки О. При перенесенні точки прикладання сили 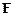 вздовж лінії її дії момент цієї сили відносно одної й тої ж нерухомої точки О не змінюється. Якщо лінія дії сили проходить через точку О, то момент сили відносно цієї точки дорівнює нулеві.
вздовж лінії її дії момент цієї сили відносно одної й тої ж нерухомої точки О не змінюється. Якщо лінія дії сили проходить через точку О, то момент сили відносно цієї точки дорівнює нулеві.
Головним моментом системи сил відносно нерухомої точки О (полюса) називається вектор 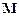 , рівний геометричній сумі моментів відносно точки О всіх n сил системи:
, рівний геометричній сумі моментів відносно точки О всіх n сил системи:
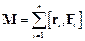 ,
,
де  – радіус-вектор, проведений із полюса О в точку прикладання сили
– радіус-вектор, проведений із полюса О в точку прикладання сили 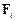 .
.
Із третього закону Ньютона випливає, що моменти відносно полюса О внутрішніх сил взаємодії матеріальних точок системи попарно компенсуються: 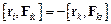 . Отже, при обчисленні головного моменту сил слід враховувати тільки зовнішні сили, що діють на розглядувану механічну систему.
. Отже, при обчисленні головного моменту сил слід враховувати тільки зовнішні сили, що діють на розглядувану механічну систему.
Моментом сили 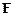 відносно нерухомої осі а називається скалярна величина
відносно нерухомої осі а називається скалярна величина 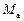 , рівна проекції на цю вісь вектора
, рівна проекції на цю вісь вектора 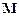 моменту сили
моменту сили 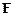 відносно довільної точки О осі а. Значення моменту
відносно довільної точки О осі а. Значення моменту 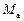 не залежить від вибору положення точки О осі а.
не залежить від вибору положення точки О осі а.
(Примітка. Іноді під моментом сили відносно нерухомої осі а розуміють векторну величину 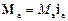 , де
, де 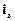 – орт осі а. Вектор
– орт осі а. Вектор 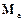 – складова вектора
– складова вектора 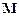 моменту сили відносно полюса О, спрямована вздовж осі а.)
моменту сили відносно полюса О, спрямована вздовж осі а.)
Якщо лінія дії сили перетинає вісь або паралельна їй, то момент сили відносно цієї осі дорівнює нулю.
 Нехай А – точка прикладання сили
Нехай А – точка прикладання сили 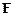 , а O1 – основа перпендикуляра, опущеного з точки А на оглядувану вісь OZ (рис. 4.2). Силу
, а O1 – основа перпендикуляра, опущеного з точки А на оглядувану вісь OZ (рис. 4.2). Силу 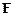 зручно розкласти на три взаємно перпендикулярні складові: осьову
зручно розкласти на три взаємно перпендикулярні складові: осьову 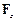 - паралельну (сулежну) осі, радіальну
- паралельну (сулежну) осі, радіальну 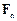 - напрямлену вздовж вектора
- напрямлену вздовж вектора 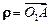 , і дотичну
, і дотичну 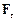 - спрямовану перпендикулярно до осі і до вектора
- спрямовану перпендикулярно до осі і до вектора 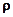 . Момент сили
. Момент сили 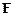 відносно осі OZ
відносно осі OZ
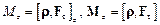 .
.
Оскільки вектори 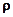 і
і 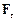 взаємно перпендикулярні, то
взаємно перпендикулярні, то
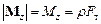 .
.
Головний момент системи сил відносно нерухомої осі дорівнює алгебраїчній сумі моментів відносно цієї осі всіх сил системи.
Моментом імпульсу (моментом кількості руху) матеріальної точки відносно нерухомої точки О (полюса) називається вектор 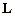 , що дорівнює векторному добуткові радіуса-вектора
, що дорівнює векторному добуткові радіуса-вектора  , проведеного з полюса О в місце перебування матеріальної точки, на вектор
, проведеного з полюса О в місце перебування матеріальної точки, на вектор  її імпульсу:
її імпульсу:
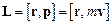 ,
,
де 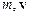 – маса і швидкість матеріальної точки.
– маса і швидкість матеріальної точки.
Моментом імпульсу системи матеріальних точок або частин твердого тіла 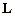 відносно нерухомої точки О називається геометрична сума моментів імпульсу відносно тієї ж точки О всіх матеріальних точок системи:
відносно нерухомої точки О називається геометрична сума моментів імпульсу відносно тієї ж точки О всіх матеріальних точок системи:
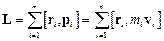 ,
,
де 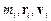 – відповідно маса, радіус-вектор і швидкість і-ї матеріальної точки, а n – загальне число цих точок у системі.
– відповідно маса, радіус-вектор і швидкість і-ї матеріальної точки, а n – загальне число цих точок у системі.
Моментом імпульсу системи відносно нерухомої осі а називається величина 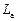 , що дорівнює проекції на цю вісь вектора
, що дорівнює проекції на цю вісь вектора 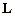 моменту імпульсу системи відносно якої-небудь точки О, яка належить цій осі:
моменту імпульсу системи відносно якої-небудь точки О, яка належить цій осі:
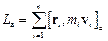 .
.
Вибір положення точки О на осі а не впливає на числове значення 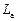 .
.
(Примітка. Іноді під моментом імпульсу системи відносно нерухомої осі а розуміють векторну величину 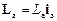 , де
, де 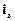 – орт осі а. )
– орт осі а. )
Момент імпульсу системи відносно нерухомої точки О, навколо якої це тіло обертається з кутовою швидкістю 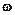 , дорівнює:
, дорівнює:
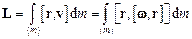 ,
,
де  – радіус-вектор, проведений із точки О в малий елемент тіла масою
– радіус-вектор, проведений із точки О в малий елемент тіла масою 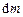 , а
, а  – швидкість цього елемента тіла. Оскільки
– швидкість цього елемента тіла. Оскільки 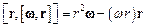 , вектори
, вектори 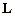 і
і 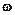 в загальному випадку не збігаються за напрямком:
в загальному випадку не збігаються за напрямком:
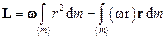 .
.
Момент імпульсу тіла, закріпленого в точці О, і його кутова швидкість збігаються за напрямком, якщо тіло обертається навколо однієї з його головних осей інерції
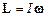 ,
,
де 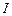 – момент інерції тіла відносно цієї головної осі.
– момент інерції тіла відносно цієї головної осі.
Значення 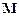 і
і 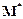 головного моменту системи сил відносно двох різних нерухомих точок О та О* пов’язані співвідношенням:
головного моменту системи сил відносно двох різних нерухомих точок О та О* пов’язані співвідношенням:
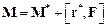 ,
,
де 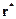 – радіус-вектор, проведений із початку О в точку О*, а
– радіус-вектор, проведений із початку О в точку О*, а 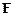 – головний вектор розглядуваної системи сил. Якщо
– головний вектор розглядуваної системи сил. Якщо 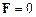 , то головний момент системи сил однаковий відносно будь-якої нерухомої точки:
, то головний момент системи сил однаковий відносно будь-якої нерухомої точки: 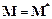 . Саме таку властивість має пара сил, тобто система з двох сил, які чисельно дорівнюють одна одній і спрямовані вздовж паралельних прямих у протилежні сторони. Найкоротша відстань
. Саме таку властивість має пара сил, тобто система з двох сил, які чисельно дорівнюють одна одній і спрямовані вздовж паралельних прямих у протилежні сторони. Найкоротша відстань 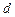 між лініями дії сил пари називається плечем пари. Момент пари сил напрямлений перпендикулярно до площини, в якій лежать сили, а його модуль дорівнює
між лініями дії сил пари називається плечем пари. Момент пари сил напрямлений перпендикулярно до площини, в якій лежать сили, а його модуль дорівнює 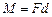 , де
, де 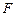 – модуль кожної з сил пари.
– модуль кожної з сил пари.
Головний момент 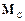 відносно центра інерції С механічної системи всіх діючих на нього сил пов’язаний з головним моментом
відносно центра інерції С механічної системи всіх діючих на нього сил пов’язаний з головним моментом 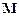 цієї ж системи сил відносно нерухомої точки О співвідношенням:
цієї ж системи сил відносно нерухомої точки О співвідношенням:
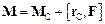 ,
,
де 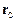 – радіус-вектор, проведений із початку О в точку С,
– радіус-вектор, проведений із початку О в точку С, 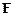 – головний вектор системи сил.
– головний вектор системи сил.
Значення моменту імпульсу механічної системи відносно її центра інерції С для абсолютного руху точок зі швидкостями 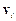 (тобто відносно нерухомої інерційної системи відліку) і для їх відносного руху зі швидкостями
(тобто відносно нерухомої інерційної системи відліку) і для їх відносного руху зі швидкостями 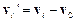 (тобто відносно системи відліку з початком у точці С, що рухається поступально) однакові:
(тобто відносно системи відліку з початком у точці С, що рухається поступально) однакові:
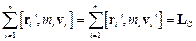 ,
,
де  – радіус-вектор і-ї точки в системі відліку, що рухається разом із центром інерції.
– радіус-вектор і-ї точки в системі відліку, що рухається разом із центром інерції.
Зв’язок між значеннями моменту імпульсу механічної системи 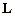 відносно нерухомої точки О і відносно центра інерції
відносно нерухомої точки О і відносно центра інерції  має вигляд:
має вигляд:
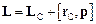 ,
,
де 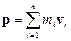 – імпульс системи в його абсолютному русі.
– імпульс системи в його абсолютному русі.
Дата добавления: 2015-04-07; просмотров: 6090;
