Вектор момента силы относительно точки
Момент силы F относительно точки О изображается вектором MО(F), приложенным в этой точке и направленным перпендикулярно к плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу F, стремящейся вращать эту плоскость в сторону, обратную вращению часовой стрелки (рис. 1.38).
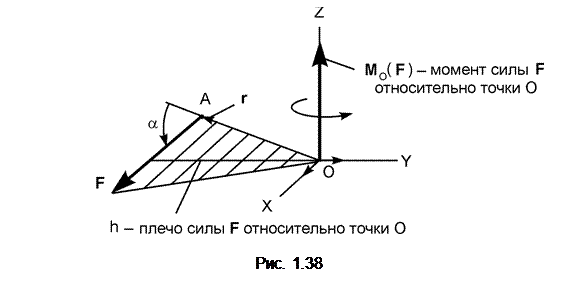 |
Модуль MО(F) этого вектора (MО(F)) равен произведению модуля F силы F на её плечо h относительно точки О. MО(F) = F×h. Сила F приложена в точке А горизонтальной плоскости OXY и параллельна координатной оси ОХ. Плечо h является кратчайшим расстоянием от этой точки до линии действия силы, то есть длиной перпендикуляра, опущенного из точки на линию действия силы.
Если из точки О в точку А приложения силы F провести радиус-вектор r, то вектор момента силы относительно точки можно выразить следующим векторным произведением:
MО(F) = r ´ F; MО(F) = r×F×sin(r, F) = r×F×sin(a) = F×h.
Дата добавления: 2015-05-30; просмотров: 1580;
