Пара сил
Пару сил в механике рассматривают как одно из основных понятий, наряду с понятием силы.
Пара сил – система двух параллельных, противоположно направленных и равных по модулю сил, не лежащих на одной прямой.
Плоскость действия пары сил – плоскость, в которой находятся линии действия сил.
Плечо пары сил – кратчайшее расстояние (длина перпендикуляра) между линиями действия сил, составляющих пару сил.
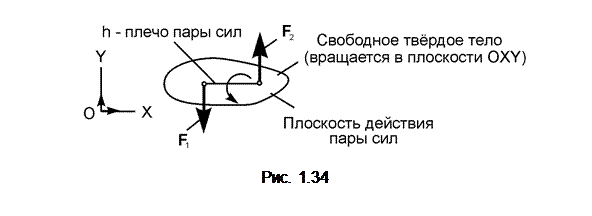
На рис. 1.34 изображена пара сил, плоскость действия которой лежит в плоскости OXY системы отсчёта OXY.
Силы F1, F2 образуют пару сил. F1 = F2; F1 = – F2. Однако силы пары не уравновешиваются, так как они направлены не по одной прямой. Пара сил стремится произвести вращение тела, к которому она приложена. Действие пары сил на тело характеризуется её моментом.
 |
Для количественной характеристики действия пары сил на тело и указания направления, в котором пара сил стремится вращать тело, вводится понятие алгебраического момента пары сил.
Алгебраический момент пары сил – величина, равная взятому с соответствующим знаком произведению модуля одной из сил на её плечо.
M = ± F1·h = ± F2·h.
Алгебраический момент пары сил считают положительным, если пара сил стремится повернуть тело против вращения часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. В системе СИ момент пары сил измеряется в Н·м.
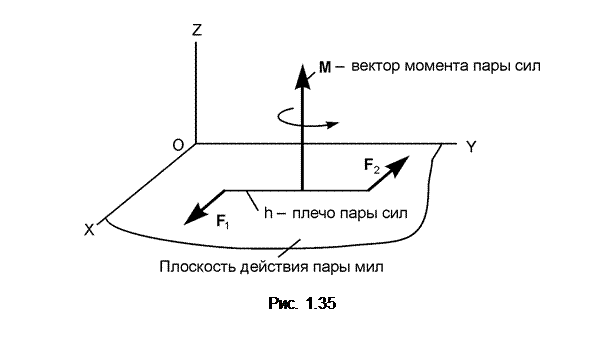 |
На рис. 1. 35 изображена пара сил (F1, F2), линии действия которых лежат в плоскости OXY.
Момент пары сил – векторная мера механического действия пары сил, равная моменту одной из сил пары относительно точки приложения другой силы.
Момент пары сил изображается вектором М. Вектор момента М пары сил (F1, F2) направлен перпендикулярно к плоскости действия пары сил в сторону, откуда видно пару сил, стремящуюся вращать плоскость её действия в сторону, противоположную вращению часовой стрелки. Согласно определению (см. рис. 1.35), M^ j, M^ i, M = F1×h = F2·h. Таким образом, пара сил полностью характеризуется её моментом M.
Теорема. Пары сил, лежащие в одной плоскости, эквивалентны, если их алгебраические моменты численно равны и одинаковы по знаку.
Доказательство этой теоремы несложно и здесь оно не приводится.
Следствия из теоремы:
1.Пару сил, не изменяя её действия на тело, можно как угодно поворачивать и переносить в любое место плоскости её действия.
2.У пары сил можно изменять плечо и модуль силы, сохраняя при этом алгебраический момент пары и плоскость действия.
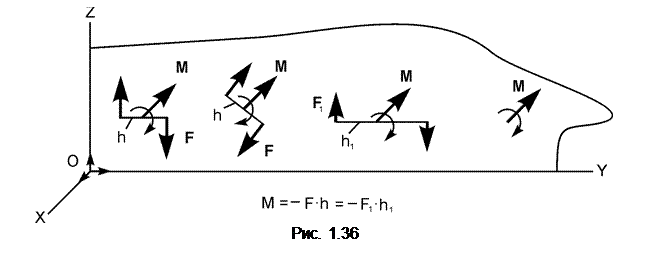
Суть теоремы и её следствий иллюстрируется рис. 1.36, на котором приведены пары сил с эквивалентными алгебраическими и векторными моментами. Плоскости действия пар сил совпадают с плоскостью YOZ.
Теорема. Пары сил в пространстве эквивалентны, если их моменты геометрически равны.
Доказательство этой теоремы также достаточно просто и здесь не приведено.
Из теорем о парах сил следует вывод: не изменяя действия пары сил на тело, пару сил можно переносить в любую плоскость, параллельную плоскости её действия, а также изменять её силу и плечо, сохраняя неизменными модуль и направление её момента.
Таким образом, вектор момента пары сил можно переносить в любую точку, то есть момент пары сил является свободным вектором.
Вектор момента пары сил определяет три элемента: положение плоскости действия пары; направление вращения; числовое значение (модуль) момента.
Отметим аналогию: если точку приложения вектора силы можно помещать где угодно на линии действия этой силы (скользящий вектор), то векторный момент пары сил можно приложить в любой точке тела (свободный вектор).
Дата добавления: 2015-05-30; просмотров: 2466;
