Потенціальна енергія

Потенціальною енергією називається частина енергії механічної системи, яка залежить тільки від її конфігурації, тобто від взаємного розташування всіх частинок (матеріальних точок), а також від їх положення в зовнішньому потенціальному полі. Зменшення потенціальної енергії при переміщенні системи з довільного положення 1 в інше довільне положення 2 вимірюється тією роботою 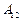, яку виконують при цьому всі потенціальні сили (внутрішні та зовнішні), що діють на систему,

,

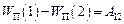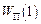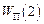де і – значення потенціальної енергії системи в початковому та кінцевому положеннях. Відповідно робота потенціальних сил при малій зміні конфігурації системи .

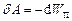У найпростішому випадку, коли система являє собою матеріальну точку, що перебуває в потенціальному полі, зв¢язок між силою , яка діє на точку, і потенціальною енергією 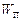цієї точки в полі має вигляд

, ,

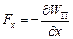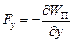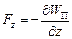
У векторному аналізі часто застосовують так званий оператор набла, який у прямокутних декартових координатах визначається як

.

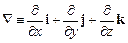Результат дії цього оператора на яку-небудь скалярну функцію 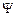просторових координат ( ) називається градієнтом цієї функції. Градієнт позначається 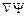або 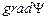. Градієнт – це вектор, модуль якого дорівнює найбільшому значенню похідної по шляху у даній точці, а напрямок градієнта збігається з напрямком, у якому це найбільше значення похідної досягається. Отже, вище отримані важливі співвідношення між зміною потенціальної енергії по координатах і силою часто записують у скороченій векторній формі

,

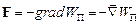тобто сила дорівнює градієнту потенціальної енергії із знаком мінус.

Отримані співвідношення дозволяють знайти залежність потенціальної енергії системи від її конфігурації тільки з точністю до довільного постійного доданка, який не впливає на зміну енергії. Для одержання залежності потенціальної енергії системи від його конфігурації в кожній конкретній задачі вибирають так звану нульову конфігурацію, в якій потенціальну енергію системи умовно вважають рівною нулеві. Таким чином, потенціальна енергія системи в довільному стані дорівнює роботі, виконуваній усіма діючими на систему потенціальними силами при переведенні системи із розглядуваного стану в стан, який відповідає нульовій конфігурації.

Приклад 1. Потенціальна енергія матеріальної точки в однорідному силовому полі. Нехай сила , що діє на точку з боку поля, напрямлена вздовж осі OZ, тобто 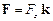, де 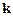– орт осі OZ, а проекція сили на вісь OZ не залежить від координат точки. Іншими словами, в усіх точках простору сила однакова і спрямована вздовж осі OZ. Тод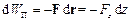і

і ,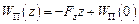

де 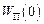– значення потенціальної енергії матеріальної точки на рівні 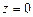. Зокрема, потенціальна енергія матеріальної точки масою 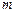, яка знаходиться в однорідному полі сили тяжіння біля поверхні Землі (вісь OZ напрямлена вертикально вгору, 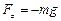, 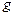– прискорення вільного падіння), дорівнює

.

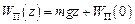Приклад 2. Потенціальна енергія матеріальної точки в полі центральних сил. У потенціальному полі центральних сил на матеріальну точку діють сили , які скрізь напрямлені вздовж прямих, що проходять через одну й ту ж нерухому точку – центр (осередок) сил, і залежать лише від відстані r до центра сил:

.

Тут – радіус-вектор, проведений із центра сил у розглядувану точку поля, а – проекція сили на напрямок вектора , яка залежить лише від відстані 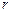. Якщо матеріальна точка притягується до центра сил, то , якщо ж вона відштовхується від осередка сил, то 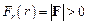. Елементарна робота сили

.

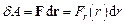Потенціальна енергія матеріальної точки

.

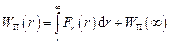Зазвичай за початок відліку потенціальної енергії приймають енергію матеріальної точки, віддалену на нескінченно велику відстань від центра сил, тобто покладають :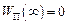

.

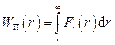Прикладами центрального силового поля, в якому сила обернено пропорційна квадратові відстані до осередка сил, F(r) 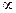r^-–2, можуть бути гравітаційні поля матеріальної точки та однорідної кулі, електростатичні поля точкового заряду, а також сфери та кулі, рівномірно заряджених відповідно по поверхні та по об¢єму.

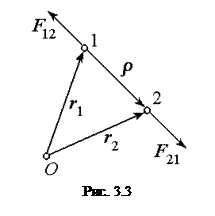
Приклад 3. Потенціальна енергія системи з двох матеріальних точок, між якими діють центральні сили, тобто сили, які залежать від відстані між точками і спрямовані вздовж прямої, що їх з¢єднує. На рис. 3.3 показані сили взаємного відштовхування 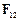і :

,

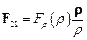де 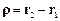– радіус-вектор, проведений із точки 1 у точку 2, а 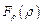– проекція сили 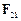на напрямок вектора 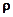, яка залежить лише від відстані 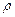між точками. Мала зміна потенціальної енергії системи

.

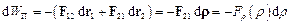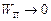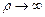Якщо прийняти, що при , то

.

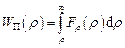Цю енергію часто називають взаємною потенціальною енергією двох матеріальних точок.

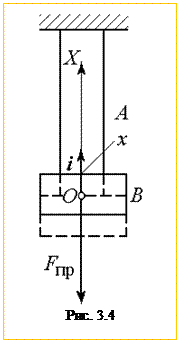
Приклад 4. Потенціальна енергія пружного тіла (наприклад, пружини) при його поздовжному розтягненні чи стисненні. При деформації пружного тіла в ньому виникають потенціальні внутрішні сили (сили пружності), які перешкоджають деформації. За законом Гука, пружна сила 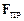, з якою деформовуване тіло А (рис. 3.4) діє на тіло В, яке спричиняє його деформацію, пропорційна величині деформації:

.

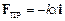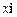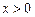Тут – вектор переміщення тіла В, який характеризує деформацію тіла А (в недеформованому стані , при стисненні , а при розтягненні 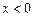), 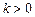– коефіцієнт (множень), що характеризує пружні властивості тіла А.

Легко отримати, що потенціальна енергія деформованого тіла

.

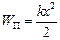Тут прийнято, що за відсутності деформації, тобто при , потенціальна енергія дорівнює нулеві.