Перетворення Галілея. Механічний принцип відносності
Перетвореннями Галілея називаються перетворення координат і часу, які застосовуються в ньютонівській механіці при переході від однієї інерційної системи відліку  до іншої
до іншої 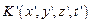 , яка рухається відносно К поступально зі сталою швидкістю
, яка рухається відносно К поступально зі сталою швидкістю  . Перетворення Галілея спираються на аксіоми про абсолютність проміжков часу і довжин. Перша аксіома стверджує, що хід часу (відповідно проміжок часу між якими-небудь двома подіями) однаковий у всіх інерційних системах відліку. Відповідно до другої аксіоми, розміри тіла не залежать від швидкості його руху відносно системи відліку.
. Перетворення Галілея спираються на аксіоми про абсолютність проміжков часу і довжин. Перша аксіома стверджує, що хід часу (відповідно проміжок часу між якими-небудь двома подіями) однаковий у всіх інерційних системах відліку. Відповідно до другої аксіоми, розміри тіла не залежать від швидкості його руху відносно системи відліку.
 Якщо відповідні осі декартових координат інерційних систем відліку
Якщо відповідні осі декартових координат інерційних систем відліку 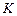 і
і 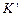 проведені попарно паралельно одна одній і якщо в початковий момент часу (
проведені попарно паралельно одна одній і якщо в початковий момент часу ( 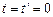 ) початки координат
) початки координат 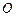 та
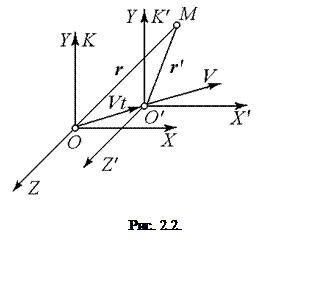
та 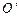 збігаються (рис. 2.2), то перетворення Галілея мають вигляд
збігаються (рис. 2.2), то перетворення Галілея мають вигляд
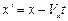 ,
, 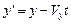 ,
,
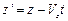 і
і 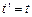 ,
,
або
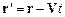 і
і 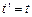 ,
,
де  і
і 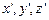 – координати точки М у системах відліку
– координати точки М у системах відліку 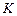 і
і 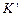 ,
,  і
і  – радіуси-вектори точки М у тих же системах віділіку, а
– радіуси-вектори точки М у тих же системах віділіку, а 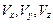 – проекції швидкості
– проекції швидкості  системи
системи 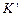 на осі координат системи
на осі координат системи 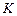 .
.
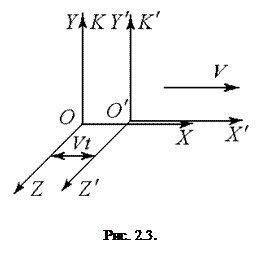
Зазвичай осі координат проводять так, що система 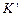 рухається вздовж додатного напрямку осі ОХ (рис. 2.3). У цьому випадку перетворення Галілея мають найпростіший вигляд:
рухається вздовж додатного напрямку осі ОХ (рис. 2.3). У цьому випадку перетворення Галілея мають найпростіший вигляд:
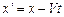 ,
, 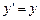 ,
, 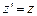 ,
, 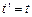 .
.
Із перетворень Галілея випливає такий закон перетворення швидкості довільної точки М (рис. 2.2) при переході від однієї інерційної системи відліку 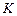 (швидкість точки
(швидкість точки 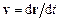 ) до іншої
) до іншої 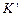 (швидкість тієї ж точки
(швидкість тієї ж точки 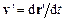 ):
):
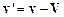 .
.
Подібним чином перетворюються і проекції швидкості на відповідні осі координат:
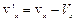 ,
, 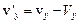 ,
, 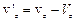 .
.
Зокрема, при русі системи К¢ вздовж додатного напрямку осі ОХ (рис. 2.3)
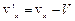 ,
, 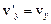 ,
, 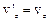 .
.
Прискорення точки М у системах відліку 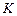 (
( 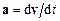 ) і
) і 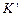 (
( 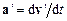 ) однакові:
) однакові: 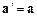 .
.
 Отже, прискорення матеріальної точки не залежить від вибору інерційної системи відліку – тобто воно інваріантне відносно перетворень Галілея.
Отже, прискорення матеріальної точки не залежить від вибору інерційної системи відліку – тобто воно інваріантне відносно перетворень Галілея.
Сили взаємодії матеріальних точок залежать лише від їх взаємного розташування і від швидкості руху однієї відносно іншої. Взаємне розташування деяких точок 2 і 1 характеризується вектором, що дорівнює різниці радіусів-векторів цих точок, тобто в системі 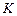 вектором
вектором 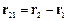 , а в системі
, а в системі 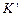 – вектором
– вектором 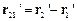 . Із перетворень Галілея випливає, що
. Із перетворень Галілея випливає, що 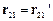 . Тому відстані між точками 1 і 2 в системах
. Тому відстані між точками 1 і 2 в системах 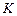 і
і 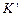 однакові:
однакові:  або
або
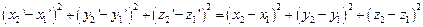 .
.
Швидкість руху точки 2 відносно точки 1 дорівнює різниці швидкостей цих точок: 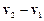 (у системі
(у системі 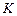 ) і
) і 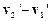 (у системі
(у системі 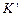 ). Із перетворень Галілея випливає, що
). Із перетворень Галілея випливає, що 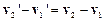 . Отже, взаємне розташування і швидкість відносного руху будь-яких двох матеріальних точок не залежить від вибору інерційної системи відліку: вони інваріантні відносно перетворень Галілея. Відповідно інваріантні відносно перетворень Галілея і сили, які діють на матеріальну точку:
. Отже, взаємне розташування і швидкість відносного руху будь-яких двох матеріальних точок не залежить від вибору інерційної системи відліку: вони інваріантні відносно перетворень Галілея. Відповідно інваріантні відносно перетворень Галілея і сили, які діють на матеріальну точку: 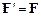 .
.
Рівняння, які виражають закони Ньютона, інваріантні відносно перетворень Галілея, тобто не змінюють свого вигляду при перетворенні координат і часу однієї інерційної системи відліку ( 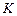 ) на іншу (
) на іншу ( 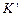 ):
):
 (в системі
(в системі 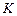 ),
),
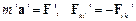 (в системі
(в системі 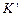 ),
),
де 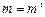 – маса розглядуваної матеріальної точки, однакова у всіх системах відліку.
– маса розглядуваної матеріальної точки, однакова у всіх системах відліку.
Таким чином, у класичній механіці справедливим є механічний принцип відносності (принцип відносності Галілея): закони механіки однакові в усіх інерційних системах відліку. Це означає, що в різних інерційних системах відліку всі механічні процеси за одних і тих же умов відбуваються однаково. Отже, за допомогою будь-яких механічних експериментів, проведених у замкненій механічній системі тіл, неможливо встановити, перебуває ця система в стані спокою чи рухається рівномірно і прямолінійно (відносно якої-небудь інерційної системи відліку).
Механічний принцип відносності свідчить про те, що в механіці всі інерційні системи відліку цілковито рівноправні. Серед них неможливо вказати якусь особливу, “головну” інерційну систему відліку, рух тіл відносно якої можна було б розглядати як “абсолютний рух”.
Узагальнення принципу відносності щодо всіх фізичних явищ було здійснено А.Ейнштейном у спеціальній теорії відносності. При цьому з¢ясувалося, що координати і час у різних інерційних системах відліку пов¢язані перетвореннями Лоренца, а не Галілея. Проте при малих швидкостях відносного руху систем відліку (порівняно зі швидкістю світла у вакуумі) перетворення Лоренца переходять у перетворення Галілея.
Дата добавления: 2015-04-07; просмотров: 4537;
