Енергія, робота і потужність
Енергією називається скалярна величина, що є мірою різних форм руху і взаємодії матерії, які розглядаються у фізиці. Енергія системи кількісно характеризує останню стосовно можливих у ній перетворень руху. Ці перетворення відбуваються завдяки взаємодії частин системи як однієї з іншою, так з зовнішніми тілами (зовнішнім середовищем). Для аналізу якісно відмінних форм руху і відповідних їм взаємодій у фізиці вводять різні види (форми) енергії: механічну, внутрішню, електромагнітну, ядерну і т.д.
Зміна механічного руху тіла зумовлюється силами, які діють на нього з боку інших тіл. Для кількісного опису такого процесу обміну енергією між тілами, що взаємодіють, у механіці користуються поняттям роботи сили, прикладеної до розглядуваного тіла. Елементарною роботою сили  на малому переміщенні
на малому переміщенні 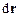 називається скалярна величина
називається скалярна величина
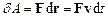 ,
,
де  і
і 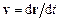 – відповідно радіус-вектор і швидкість точки прикладання сили, а
– відповідно радіус-вектор і швидкість точки прикладання сили, а 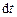 – малий проміжок часу, за який сила
– малий проміжок часу, за який сила  виконує роботу
виконує роботу 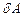 . У прямокутних декартових координатах скалярний добуток векторів можна представити так:
. У прямокутних декартових координатах скалярний добуток векторів можна представити так:
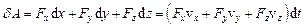 ,
,
де  – координати точки прикладання сили, а
– координати точки прикладання сили, а 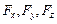 і
і 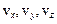 – проекції на осі координат векторів
– проекції на осі координат векторів  і
і  .
.
Вираз для елементарної роботи можна також подати у вигляді
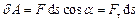 ,
,
де  – елементарна довжина шляху точки прикладання сили за розглядуваний малий проміжок часу
– елементарна довжина шляху точки прикладання сили за розглядуваний малий проміжок часу 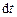 ,
, 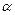 – кут між векторами
– кут між векторами  і
і 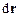 . а
. а 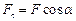 – проекція сили на напрямок переміщення
– проекція сили на напрямок переміщення 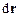 . Тоді стає очевидним, що сила, нормальна до траєкторії точки її прикладання, роботи не виконує.
. Тоді стає очевидним, що сила, нормальна до траєкторії точки її прикладання, роботи не виконує.
Силу  називають рушійною силою, якщо
називають рушійною силою, якщо  , так що
, так що 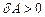 . Якщо ж
. Якщо ж 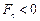 , то
, то 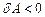 , і тоді силу
, і тоді силу  називають гальмувальною силою (силою опору).
називають гальмувальною силою (силою опору).
Якщо на механічну систему одночасно діють сили 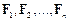 , то робота
, то робота 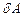 , виконувана ними за малий час
, виконувана ними за малий час 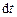 , дорівнює алгебраїчній сумі робіт, здійснюваних за той же час
, дорівнює алгебраїчній сумі робіт, здійснюваних за той же час 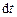 кожною із них окремо,
кожною із них окремо,
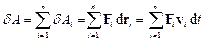 ,
,
де 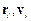 – радіус-вектор і швидкість точки прикладання сили
– радіус-вектор і швидкість точки прикладання сили 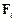 .
.
Наприклад, для матеріальної точки 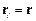 – радіус-вектор цієї точки, а
– радіус-вектор цієї точки, а 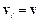 – її швидкість. Відповідно
– її швидкість. Відповідно 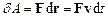 , де
, де  – рівнодійна сила. Із другого закону Ньютона випливає, що для матеріальної точки
– рівнодійна сила. Із другого закону Ньютона випливає, що для матеріальної точки
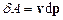 ,
,
де 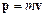 – імпульс точки,
– імпульс точки, 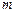 – її маса.
– її маса.
У випадку поступального руху абсолютно твердого тіла 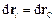 і
і 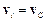 , де
, де 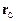 і
і 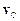 – радіус-вектор і швидкість центра інерції тіла.
– радіус-вектор і швидкість центра інерції тіла.
Робота внутрішніх сил при будь-якому русі абсолютно твердого тіла дорівнює нулеві. Тому при поступальному русі такого тіла 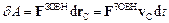 , де
, де 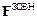 – головний вектор зовнішніх сил. Із закону руху центра інерції випливає, що
– головний вектор зовнішніх сил. Із закону руху центра інерції випливає, що
 ,
,
де 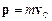 – імпульс твердого тіла масою m, яке рухається поступально зі швидкістю
– імпульс твердого тіла масою m, яке рухається поступально зі швидкістю 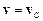 .
.
 Робота
Робота 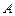 , виконувана силою
, виконувана силою  на скінченній ділянці траєкторії
на скінченній ділянці траєкторії 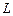 точки її прикладання, дорівнює алгебраїчній сумі робіт на всіх малих частинах цієї ділянки, тобто виражається криволінійним інтегралом
точки її прикладання, дорівнює алгебраїчній сумі робіт на всіх малих частинах цієї ділянки, тобто виражається криволінійним інтегралом
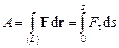 ,
,
де 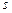 – довжина шляху, відлічувана вздовж траєкторії від початку розглядуваної ділянки,
– довжина шляху, відлічувана вздовж траєкторії від початку розглядуваної ділянки, 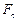 – проекція сили на напрямок переміщення
– проекція сили на напрямок переміщення 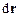 точки її прикладання. Для обчислення цього інтегралу необхідно знати залежність
точки її прикладання. Для обчислення цього інтегралу необхідно знати залежність 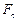 від
від 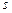 вздовж даної траєкторії
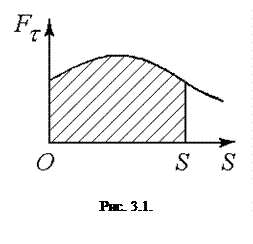
вздовж даної траєкторії 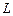 . Якщо ця залежність представлена графічно (рис. 3.1), то робота
. Якщо ця залежність представлена графічно (рис. 3.1), то робота  вимірюється площею, заштрихованою на рис. 3.1.
вимірюється площею, заштрихованою на рис. 3.1.
Всі сили, що зустрічаються в класичній механіці, поділяють на консервативні і неконсервативні. 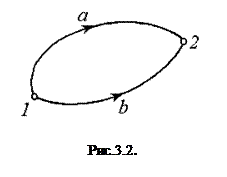 Консервативними силами називаються такі сили, робота яких залежить лише від початкових і кінцевих положень точок їх прикладання і не залежить ні від виду траєкторій цих точок, ні від законів їх руху по траєкторіях. Наприклад, сили взаємодії частин системи (матеріальних точок) консервативні, якщо вони залежать тільки від конфігурації системи, тобто від взаємного розташування всіх точок системи, причому робота цих сил при переміщенні системи з одного довільного положенні в інше не залежить від способу переміщення, а повністю визначається початковою та кінцевою конфігураціями системи. Прикладами подібих сил можуть бути сили гравітаційної взаємодії. Робота сили тяжіння не залежить від форми шляху, а визначається лише початковим та кінцевим положенням тіла, що переміщується.
Консервативними силами називаються такі сили, робота яких залежить лише від початкових і кінцевих положень точок їх прикладання і не залежить ні від виду траєкторій цих точок, ні від законів їх руху по траєкторіях. Наприклад, сили взаємодії частин системи (матеріальних точок) консервативні, якщо вони залежать тільки від конфігурації системи, тобто від взаємного розташування всіх точок системи, причому робота цих сил при переміщенні системи з одного довільного положенні в інше не залежить від способу переміщення, а повністю визначається початковою та кінцевою конфігураціями системи. Прикладами подібих сил можуть бути сили гравітаційної взаємодії. Робота сили тяжіння не залежить від форми шляху, а визначається лише початковим та кінцевим положенням тіла, що переміщується.
Стаціонарне поле називається потенціальним, якщо сила  , із якою воно діє на поміщену в нього матеріальну точку, консервативна. Це означає, що сила
, із якою воно діє на поміщену в нього матеріальну точку, консервативна. Це означає, що сила  залежить лише від положення матеріальної точки в полі, а робота сили
залежить лише від положення матеріальної точки в полі, а робота сили  при переміщенні точки з одного довільного положення 1 в інше – 2 (рис. 3.2) вздовж будь-яких двох траєкторій, наприклад, 1а2 (робота
при переміщенні точки з одного довільного положення 1 в інше – 2 (рис. 3.2) вздовж будь-яких двох траєкторій, наприклад, 1а2 (робота  ) і 1b2 (робота
) і 1b2 (робота 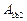 ) однакова:
) однакова:
 .
.
Відповідно робота консервативної сили при переміщенні точки її прикладання вздовж будь-якої замкненої траєкторії 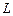 (наприклад, 1а2b1) дорівнює нулю:
(наприклад, 1а2b1) дорівнює нулю:
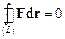 .
.
Всі сили, що не є консервативними, називаються неконсервативними силами. До неконсервативних сил відносяться дисипативні та гіроскопічні сили.
Дисипативними силами називаються сили, сумарна робота яких при будь-яких переміщеннях замкненої системи завжди від¢ємна. До них належать, наприклад, сили тертя, які виникають при ковзанні якого-небудь тіла по поверхні іншого. Дисипативні сили, на відміну від консервативних, залежать не тільки від взаємного розташування тіл взаємодії, але також і від їх відносних швидкостей. Ці сили завжди спрямовані проти напрямку швидкості тіла відносно поверхні (або середовища), по якій воно рухається.
Гіроскопічними силами називаються сили, що залежать від швидкості матеріальної точки, на яку вони діють, і напрямлені перпендикулярно до цієї швидкості. Прикладом гіроскопічної сили є сила Лоренца, яка діє з боку магнітного поля на заряджену частинку, що рухається в ньому. Робота гіроскопічних сил завжди нульова незалежно від того, як переміщується матеріальна точка.
Елементарну роботу сили  , що діє на матеріальну точку з боку стаціонарного потенціального поля, можна представити у вигляді повного диференціала скалярної функції координат
, що діє на матеріальну точку з боку стаціонарного потенціального поля, можна представити у вигляді повного диференціала скалярної функції координат 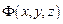 , яка називається силовою функцією цього поля:
, яка називається силовою функцією цього поля:
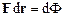 , або
, або 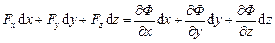 .
.
Отже,
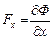 ,
, 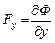 ,
, 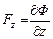 .
.
Елементарну роботу непотенціальної сили не можна представити у вигляді повного диференціала якої-небудь функції координат. Саме тому елементарна робота довільної сили позначена не 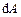 , а
, а 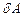 .
.
Для характеристики роботи, виконуваної за одиницю часу, в механіці користуються поняттям потужності. Потужністю (миттєвою потужністю) називається скалярна фізична величина 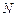 , рівна відношенню елементарної роботи
, рівна відношенню елементарної роботи 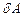 до малого проміжку часу
до малого проміжку часу 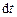 , протягом якого ця робота виконується,
, протягом якого ця робота виконується,
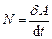 .
.
Якщо  – сила, що виконує роботу
– сила, що виконує роботу 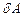 , то потужність дорівнює скалярному добутку сили
, то потужність дорівнює скалярному добутку сили  на швидкість
на швидкість  точки її прикладання:
точки її прикладання:
 .
.
У загальному випадку потужність може змінюватися з часом.
Середньою потужністю в інтервалі від t до 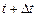 називається фізична величина
називається фізична величина 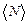 , яка дорівнює відношеню роботи
, яка дорівнює відношеню роботи 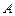 , виконуваної за цей проміжок часу, до його тривалості
, виконуваної за цей проміжок часу, до його тривалості 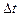 :
:
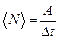 .
.
Дата добавления: 2015-04-07; просмотров: 2348;
