Третій закон Ньютона. Рух центра інерції
Механічний вплив тіл одне на одне має характер взаємодії. Про це говорить третій закон Ньютона: дві матеріальні точки діють одна на іншу з силами, які чисельно рівні і напрямлені в протилежні сторони вздовж прямої, яка проходить через ці точки.
Якщо 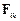 – сила, що діє на і-у матеріальну точку з боку k-ї, а
– сила, що діє на і-у матеріальну точку з боку k-ї, а 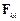 – сила, що діє на k-у матеріальну точку з боку і-ї, то, відповідно до третього закону Ньютона,
– сила, що діє на k-у матеріальну точку з боку і-ї, то, відповідно до третього закону Ньютона,
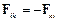 .
.
Сили 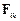 і
і 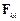 прикладені до різних матеріальних точок і можуть взаємно зрівноважуватися тільки в тих випадках, коли ці точки належать одному й тому ж твердому тілу.
прикладені до різних матеріальних точок і можуть взаємно зрівноважуватися тільки в тих випадках, коли ці точки належать одному й тому ж твердому тілу.
Третій закон Ньютона є істотним доповненням до першого та другого законів. Він дозволяє перейти від динаміки окремої матеріальної точки до силоруху довільної механічної системи. Із третього закону Ньютона випливає, що в будь-якій механічній системі геометрична сума всіх внутрішніх сил дорівнює нулеві:
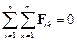 ,
,
де n – число матеріальних точок, які входять до складу системи, а 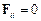 .
.
Вектор 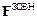 , рівний геометричній сумі всіх зовнішніх сил, які діють на систему, називається головним вектором зовнішніх сил:
, рівний геометричній сумі всіх зовнішніх сил, які діють на систему, називається головним вектором зовнішніх сил:
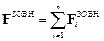 ,
,
де 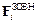 – результовна зовнішніх сил, прикладених до і-ї матеріальної точки.
– результовна зовнішніх сил, прикладених до і-ї матеріальної точки.
Із другого та третього законів Ньютона випливає, що перша похідна за часом 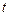 від імпульсу
від імпульсу 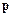 механічної системи дорівнює головному векторові всіх зовнішніх сил, прикладених до неї,
механічної системи дорівнює головному векторові всіх зовнішніх сил, прикладених до неї,
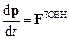 .
.
Це рівняння виражає закон зміни імпульсу системи.
Оскільки 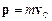 , де
, де 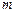 – маса системи, а
– маса системи, а 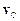 – швидкість її центра інерції, то закон руху центра інерції механічної системи має вигляд
– швидкість її центра інерції, то закон руху центра інерції механічної системи має вигляд
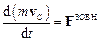 , або
, або 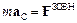 ,
,
де 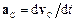 – прискорення центра інерції. Таким чином, центр інерції механічної системи рухається як матеріальна точка, маса якої дорівнює масі всієї системи, і на яку діє сила, рівна головному векторові зовнішніх сил, прикладених до системи.
– прискорення центра інерції. Таким чином, центр інерції механічної системи рухається як матеріальна точка, маса якої дорівнює масі всієї системи, і на яку діє сила, рівна головному векторові зовнішніх сил, прикладених до системи.
Якщо розглядувана система – тверде тіло, що рухається поступально, то швидкості 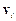 всіх точок тіла та його центра інерції
всіх точок тіла та його центра інерції 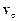 однакові і дорівнюють швидкості
однакові і дорівнюють швидкості  тіла. Відповідно прискорення тіла
тіла. Відповідно прискорення тіла 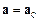 і основне рівняння динаміки поступального руху твердого тіла має вигляд
і основне рівняння динаміки поступального руху твердого тіла має вигляд
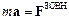 .
.
Дата добавления: 2015-04-07; просмотров: 965;
