Другий закон Ньютона
Основним законом динаміки матеріальної точки є другий закон Ньютона, який говорить про те, як змінюється механічний рух матеріальної точки під дією прикладених до неї сил. Другий закон Ньютона свідчить: швидкість зміни імпульсу 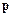 матеріальної точки дорівнює силі
матеріальної точки дорівнює силі  , що діє на неї, тобто
, що діє на неї, тобто
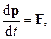 або
або 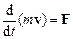 ,
,
де 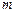 і
і  – відповідно маса і швидкість матеріальної точки.
– відповідно маса і швидкість матеріальної точки.
Якщо на матеріальну точку одночасно діють декілька сил, то під силою  у другому законі Ньютона треба розуміти геометричну суму їх усіх, тобто вислідну силу.
у другому законі Ньютона треба розуміти геометричну суму їх усіх, тобто вислідну силу.
Векторна величина 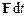 називається елементарним імпульсом сили
називається елементарним імпульсом сили  за малий час
за малий час 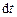 її дії. Імпульс сили
її дії. Імпульс сили  за скінченний проміжок часу від
за скінченний проміжок часу від 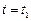 до
до 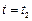 дорівнює означеному інтегралові
дорівнює означеному інтегралові 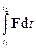 , де
, де  , у загальному випадку, залежить від часу t. Згідно з другим законом Ньютона, зміна імпульсу матеріальної точки дорівнює імпульсові сили, яка діє на неї:
, у загальному випадку, залежить від часу t. Згідно з другим законом Ньютона, зміна імпульсу матеріальної точки дорівнює імпульсові сили, яка діє на неї:
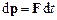 та
та 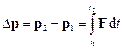 ,
,
де 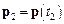 і
і 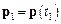 – значення імпульсу матеріальної точки в кінці (
– значення імпульсу матеріальної точки в кінці ( 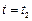 ) і на початку (
) і на початку ( 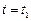 ) розглядуваного проміжку часу.
) розглядуваного проміжку часу.
Оскільки в ньютонівській механіці маса 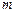 матеріальної точки не залежить від стану руху точки, то
матеріальної точки не залежить від стану руху точки, то 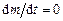 . Тому математичний вираз другого закону Ньютона можна також представити у формі
. Тому математичний вираз другого закону Ньютона можна також представити у формі
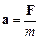 ,
,
де 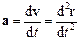 – прискорення матеріальної точки,
– прискорення матеріальної точки,  – її радіус-вектор. Відповідне формулювання другого закону Ньютона таке: прискорення матеріальної точки збігається за напрямком з діючою на неї силою і дорівнює відношенню цієї сили до маси матеріальної точки.
– її радіус-вектор. Відповідне формулювання другого закону Ньютона таке: прискорення матеріальної точки збігається за напрямком з діючою на неї силою і дорівнює відношенню цієї сили до маси матеріальної точки.
Дотичне і нормальне прискорення матеріальної точки визначаються відповідними складовими сили 
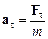 ,
, 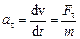
та
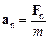 ,
, 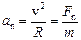 ,
,
де v – модуль вектора швидкості матеріальної точки, а 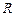 – радіус кривизни її траєкторії. Сила
– радіус кривизни її траєкторії. Сила 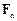 , що надає матеріальній точці нормального прискорення, напрямлена до центра кривизни траєкторії точки і тому називається доцентровою силою.
, що надає матеріальній точці нормального прискорення, напрямлена до центра кривизни траєкторії точки і тому називається доцентровою силою.
Якщо на матеріальну точку одночасно діють декілька сил 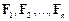 , то її прискорення визначається векторною сумою цих сил:
, то її прискорення визначається векторною сумою цих сил:
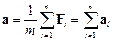 ,
,
де 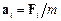 . Отже, кожна із сил, які одночасно діють на матеріальну точку, надає їй такого ж прискорення, як і за відсутності інших сил (принцип незалежності дії сил).
. Отже, кожна із сил, які одночасно діють на матеріальну точку, надає їй такого ж прискорення, як і за відсутності інших сил (принцип незалежності дії сил).
Диференціальним рівнянням руху матеріальної точки називається рівняння
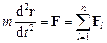 .
.
У проекціях на осі прямокутної декартової системи координат це рівняння має вигляд
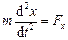 ,
, 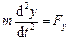 ,
, 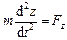 ,
,
де x, y і z – координати рухомої точки.
Дата добавления: 2015-04-07; просмотров: 995;
