Поступальний та обертальний рухи твердого тіла
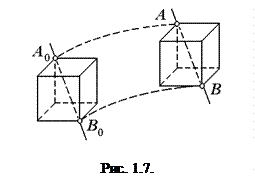 Поступальним рухом твердого тіла називається такий його рух, при якому будь-яка пряма, жорстко зв’язана з тілом – наприклад, пряма АВ на рис. 1.7 – переміщується, лишаючись завжди паралельною до осі A0B0, напрямок якої визначається початковим положенням тіла. При поступальному русі всі точки твердого тіла рухаються за однаковими траєкторіями (наприклад траєкторії АA0 і ВВ0 на рис. 1.7). Тут будемо розглядати абсолютно тверді тіла, які для стислості називатимемо просто твердими тілами. Поступально рухаються відносно Землі, наприклад, кабіна ліфта, різець токарного верстата, стрілка компаса при переміщенні його корпуса в горизонтальній площині тощо.
Поступальним рухом твердого тіла називається такий його рух, при якому будь-яка пряма, жорстко зв’язана з тілом – наприклад, пряма АВ на рис. 1.7 – переміщується, лишаючись завжди паралельною до осі A0B0, напрямок якої визначається початковим положенням тіла. При поступальному русі всі точки твердого тіла рухаються за однаковими траєкторіями (наприклад траєкторії АA0 і ВВ0 на рис. 1.7). Тут будемо розглядати абсолютно тверді тіла, які для стислості називатимемо просто твердими тілами. Поступально рухаються відносно Землі, наприклад, кабіна ліфта, різець токарного верстата, стрілка компаса при переміщенні його корпуса в горизонтальній площині тощо.
При поступальному русі твердого тіла всі його точки переміщуються цілком однаково: за малий час 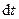 радіуси-вектори цих точок змінюються на одну й ту ж величину
радіуси-вектори цих точок змінюються на одну й ту ж величину 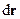 . Відповідно в кожний момент часу швидкості всіх точок тіла однакові і дорівнюють
. Відповідно в кожний момент часу швидкості всіх точок тіла однакові і дорівнюють 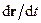 , а отже, однакові і їх прискорення. Тому кінематичний розгляд поступального руху твердого тіла зводиться до вивчення руху якоїсь із його точок. У динаміці зазвичай розглядають рух центра інерції тіла. Тверде тіло, що вільно рухається в просторі, має три поступальні ступені вільності, які відповідають його поступальному переміщенню вздовж трьох осей координат.
, а отже, однакові і їх прискорення. Тому кінематичний розгляд поступального руху твердого тіла зводиться до вивчення руху якоїсь із його точок. У динаміці зазвичай розглядають рух центра інерції тіла. Тверде тіло, що вільно рухається в просторі, має три поступальні ступені вільності, які відповідають його поступальному переміщенню вздовж трьох осей координат.
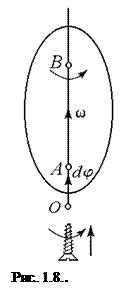 Рух твердого тіла, при якому дві його точки А і В лишаються нерухомими, називається обертанням (або обертальним рухом) тіла навколо нерухомої осі (рис.1.8). Нерухома пряма АВ називається віссю обертання тіла. При обертанні навколо нерухомої осі всі точки тіла описують кола, центри яких лежать на осі обертання, а площини перпендикулярні до неї. Подібний рух відносно Землі здійснюють, наприклад, ротори турбін, електродвигунів і генераторів, установлених нерухомо на Землі.
Рух твердого тіла, при якому дві його точки А і В лишаються нерухомими, називається обертанням (або обертальним рухом) тіла навколо нерухомої осі (рис.1.8). Нерухома пряма АВ називається віссю обертання тіла. При обертанні навколо нерухомої осі всі точки тіла описують кола, центри яких лежать на осі обертання, а площини перпендикулярні до неї. Подібний рух відносно Землі здійснюють, наприклад, ротори турбін, електродвигунів і генераторів, установлених нерухомо на Землі.
Тверде тіло, яке обертається навколо нерухомої осі, має одну ступінь вільності. Його положення в просторі повністю визначається величиною j кута повороту тіла з деякого певного (початкового) положення.
 Для характеристики хуткості і напрямку обертання тіла навколо осі служить кутова швидкість
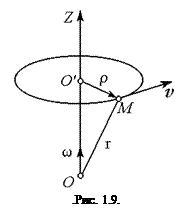
Для характеристики хуткості і напрямку обертання тіла навколо осі служить кутова швидкість  . Усі точки твердого тіла обертаються з однаковими кутовими швидкостями. Довільна точка М твердого тіла, яке обертається навколо нерухомої осі OZ з кутовою швидкістю
. Усі точки твердого тіла обертаються з однаковими кутовими швидкостями. Довільна точка М твердого тіла, яке обертається навколо нерухомої осі OZ з кутовою швидкістю  , описує коло радіусом
, описує коло радіусом 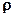 із центром у точці О¢ (рис. 1.9). Швидкість
із центром у точці О¢ (рис. 1.9). Швидкість 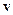 точки М, на відміну від кутової швидкості тіла, часто називають лінійною швидкістю. Вона напрямлена перпендикулярно як до осі обертання (тобто до вектора
точки М, на відміну від кутової швидкості тіла, часто називають лінійною швидкістю. Вона напрямлена перпендикулярно як до осі обертання (тобто до вектора 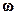 ), так і до радіуса-вектора
), так і до радіуса-вектора 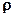 , проведеного в точку М із центра кола О¢, і дорівнює їх векторному добутку:
, проведеного в точку М із центра кола О¢, і дорівнює їх векторному добутку: 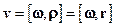 та
та 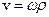 . Тут
. Тут 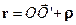 – радіус-вектор точки М, проведений із точки О осі обертання, прийнятої за початок координат.
– радіус-вектор точки М, проведений із точки О осі обертання, прийнятої за початок координат.
Рух твердого тіла, при якому одна з його точок лишається на місці, називається обертанням тіла навколо нерухомої точки. Зазвичай цю точку приймають за початок координат нерухомої системи відліку. При обертанні навколо нерухомої точки всі точки тіла рухаються по поверхнях концентричних сфер, центри яких знаходяться в нерухомій точці. У кожний момент часу такий рух тіла можна розглядати як обертання навколо деякої осі, яка проходить через нерухому точку. Цю вісь називають миттєвою віссю обертання. У загальному випадку положення миттєвої осі обертання змінюється відносно як нерухомого укладу відліку, так і системи відліку, жорстко зв’язаної з розглядуваним тілом.
Швидкість 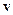 довільної точки М тіла дорівнює
довільної точки М тіла дорівнює 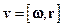 та
та 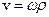 . Тут
. Тут 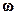 – кутова швидкість тіла, напрямлена вздовж миттєвої осі обертання,
– кутова швидкість тіла, напрямлена вздовж миттєвої осі обертання, 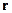 – радіус-вектор, проведений у точку М із нерухомої точки О, навколо якої обертається тіло, а
– радіус-вектор, проведений у точку М із нерухомої точки О, навколо якої обертається тіло, а 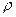 – відстань від точки М до миттєвої осі.
– відстань від точки М до миттєвої осі.
Тіло може здійснювати три незалежних рухи: обертатися навколо кожної з трьох взаємно перпендикулярних осей, які проходять через нерухому точку О. Таким чином, воно має три ступені вільності.
Для характеристики хуткості зміни вектора кутової швидкості тіла при нерівномірному обертанні тіла навколо нерухомої осі або при його обертанні навколо нерухомої точки вводиться вектор 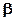 кутового прискорення тіла, що дорівнює першій похідній від його кутової швидкості w за часом t:
кутового прискорення тіла, що дорівнює першій похідній від його кутової швидкості w за часом t: 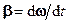 . Якщо тіло обертається навколо нерухомої осі, то вектори
. Якщо тіло обертається навколо нерухомої осі, то вектори 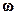 і
і 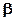 спрямовані уздовж цієї осі: при прискореному обертанні (
спрямовані уздовж цієї осі: при прискореному обертанні ( 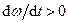 ) вектор
) вектор 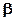 напрямлений в той же самий бік, що й
напрямлений в той же самий бік, що й 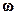 , а при сповільненому (
, а при сповільненому ( 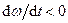 )– в протилежний.
)– в протилежний.
Проекція кутового прискорення на нерухому вісь обертання OZ рівна 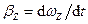 , де
, де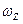 -проекція на ту ж вісь вектора
-проекція на ту ж вісь вектора 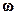 .
.
Прискорення 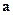 довільної точки М тіла, яке обертається навколо нерухомої точки О або нерухомої осі, що проходить через цю точку, часто називають, на відміну від кутового прискорення тіла, лінійним прискоренням. Воно дорівнює
довільної точки М тіла, яке обертається навколо нерухомої точки О або нерухомої осі, що проходить через цю точку, часто називають, на відміну від кутового прискорення тіла, лінійним прискоренням. Воно дорівнює
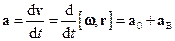 ,
,
де 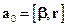 – обертальне прискорення точки, а
– обертальне прискорення точки, а 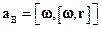 – довісне прискорення точки, спрямоване до миттєвої осі обертання. Якщо тіло обертається навколо нерухомої осі OZ (рис. 1.9), то обертальне прискорення точки М збігається з її дотичним прискоренням
– довісне прискорення точки, спрямоване до миттєвої осі обертання. Якщо тіло обертається навколо нерухомої осі OZ (рис. 1.9), то обертальне прискорення точки М збігається з її дотичним прискоренням 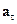 , а довісне – з нормальним прискоренням
, а довісне – з нормальним прискоренням 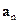 .
.
Будь-який складний рух твердого тіла можна розкласти на два простих: поступальний рух зі швидкістю 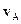 деякої довільно вибраної точки А тіла і обертання навколо миттєвої осі, яка проходить через цю точку. Кутова швидкість обертання w не залежить від вибору точки А. Швидкість довільної точки М тіла
деякої довільно вибраної точки А тіла і обертання навколо миттєвої осі, яка проходить через цю точку. Кутова швидкість обертання w не залежить від вибору точки А. Швидкість довільної точки М тіла
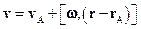 ,
,
де 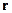 та
та 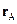 – радіуси-вектори точок М і А.
– радіуси-вектори точок М і А.
У динаміці твердого тіла зручно розглядати складний рух як сукупність двох одночасних рухів – поступального зі швидкістю центра інерції та обертання навколо центра інерції.
Найпростіший випадок складного руху тіла – плоский, або плоскопаралельний рух, при якому всі точки тіла рухаються в паралельних площинах. Такий рух здійснює, наприклад, однорідний круговий циліндр, скочуючись із похилої площини. При плоскому русі напрямок миттєвої осі обертання тіла навколо точки А не змінюється, а вектори 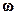 і
і 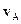 взаємноперпендикулярні.
взаємноперпендикулярні.
Дата добавления: 2015-04-07; просмотров: 4588;
