Кінематика обертального руху матеріальної точки
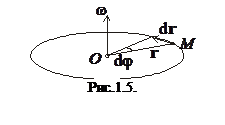 Розглянемо матеріальну точку, яка рухається по колу з центром у точці O (див. рис.1.5). Така точка має одну ступінь вільності, тобто її положення в просторі повністю визначається величиною
Розглянемо матеріальну точку, яка рухається по колу з центром у точці O (див. рис.1.5). Така точка має одну ступінь вільності, тобто її положення в просторі повністю визначається величиною 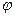 кута повороту її радіус-вектора
кута повороту її радіус-вектора 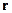 з деякого певного (початкового) положення. За проміжок часу
з деякого певного (початкового) положення. За проміжок часу 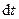 радіус-вектор точки повертається на кут
радіус-вектор точки повертається на кут 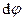 . Згідно з означенням кута як відношення дуги до радіуса, для нескінченно малих величин, очевидно, можна записати
. Згідно з означенням кута як відношення дуги до радіуса, для нескінченно малих величин, очевидно, можна записати
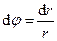 .
.
Введемо вектор 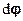 , довжина якого дорівнює куту нескінченно малого повороту гвинта
, довжина якого дорівнює куту нескінченно малого повороту гвинта 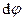 , а напрямок визначається напрямком обертання матеріальної точки згідно з правилом правого гвинта. Іншими словами, вектор
, а напрямок визначається напрямком обертання матеріальної точки згідно з правилом правого гвинта. Іншими словами, вектор 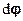 напрямлений уздовж осі обертання так, що із його кінця обертання точки видно як таке, що відбувається проти годинникової стрілки. Вектори, подібні до
напрямлений уздовж осі обертання так, що із його кінця обертання точки видно як таке, що відбувається проти годинникової стрілки. Вектори, подібні до 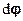 , напрямок яких пов’язується з напрямком обертання і змінюється при переході від правої системи координат до лівої, називаються псевдовекторами, або аксіальними векторами (на відміну від звичайних, полярних векторів, що не змінюють свого напрямку при такому перетворенні координат). Зауважимо, що векторний добуток двох полярних векторів є псевдовектором, а векторний добуток псевдовектора і полярного вектора – полярним вектором.
, напрямок яких пов’язується з напрямком обертання і змінюється при переході від правої системи координат до лівої, називаються псевдовекторами, або аксіальними векторами (на відміну від звичайних, полярних векторів, що не змінюють свого напрямку при такому перетворенні координат). Зауважимо, що векторний добуток двох полярних векторів є псевдовектором, а векторний добуток псевдовектора і полярного вектора – полярним вектором.
Уведений таким чином вектор 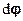 дозволяє записати просте векторне співвідношення між переміщенням і радіус-вектором
дозволяє записати просте векторне співвідношення між переміщенням і радіус-вектором
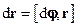 .
.
Розділимо ліву і праву частини цього рівняння на 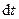 і отримаємо важливу формулу
і отримаємо важливу формулу
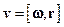 ,
,
де введено векторну величину
 .
.
яка називається кутовою швидкістю. У кінематиці обертального руху вона відіграє таку ж важливу роль, як вектор швидкості 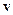 у кінематиці поступального руху.
у кінематиці поступального руху.
Аксіальні вектори 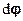 і
і 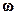 не мають певних точок прикладання: вони можуть відкладатися з будь-якої точки осі обертання. На рис.1.5 вони відкладені з деякої точки О нерухомої осі обертання, яка приймається одночасно за початок координат укладу відліку.
не мають певних точок прикладання: вони можуть відкладатися з будь-якої точки осі обертання. На рис.1.5 вони відкладені з деякої точки О нерухомої осі обертання, яка приймається одночасно за початок координат укладу відліку.
Напрямок вектора 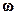 легше за все визначати за правилом правого гвинта: він збігається з напрямком поступального руху правого гвинта, який обертається разом із точкою. Наприклад, вектор кутової швидкості невеликого тіла, що лежить на поверхні Землі і обертається разом з нею навколо її осі, напрямлений уздовж осі обертання Землі у напрямку від південного полюса до північного і за модулем становить приблизно
легше за все визначати за правилом правого гвинта: він збігається з напрямком поступального руху правого гвинта, який обертається разом із точкою. Наприклад, вектор кутової швидкості невеликого тіла, що лежить на поверхні Землі і обертається разом з нею навколо її осі, напрямлений уздовж осі обертання Землі у напрямку від південного полюса до північного і за модулем становить приблизно 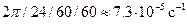 .
.
Обертання називається рівномірним, якщо числове значення кутової швидкості не змінюється з часом: 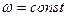 . У цьому випадку кут повороту залежить лінійно від часу:
. У цьому випадку кут повороту залежить лінійно від часу: 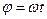 .
.
Періодом обертання називається проміжок часу 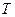 , протягом якого точка, рівномірно обертаючись із кутовою швидкістю
, протягом якого точка, рівномірно обертаючись із кутовою швидкістю 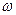 , здійснює один оберт навколо осі обертання (повертається на кут
, здійснює один оберт навколо осі обертання (повертається на кут 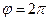 )
)
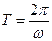 .
.
Частота обертання
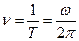
показує число обертів, здійснюваних за одиницю часу при рівномірному обертанні з кутовою швидкістю 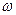 .
.
Аналогічно тому, як було введено вектор прискорення 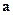 у кінематиці поступального руху, введемо ще одну векторну фізичну величину – кутове прискорення. Кутовим прискоренням називається вектор:
у кінематиці поступального руху, введемо ще одну векторну фізичну величину – кутове прискорення. Кутовим прискоренням називається вектор:
 .
.
 Шляхом диференціювання щойно отриманого виразу
Шляхом диференціювання щойно отриманого виразу 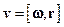 можна отримати важливе співвідношення між кутовим прискоренням
можна отримати важливе співвідношення між кутовим прискоренням  і прискоренням
і прискоренням  :
:
 .
.
Таким чином, вектор прискорення 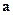 , з яким рухається точка по колу, можна подати як суму двох взаємно перпендикулярних компонент:
, з яким рухається точка по колу, можна подати як суму двох взаємно перпендикулярних компонент:
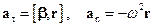 .
.
Вектор 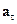 спрямований по дотичній до траєкторії, він називається дотичним, або тангенційним, прискоренням точки. Дотичне прискорення характеризує хуткість зміни модуля вектора швидкості точки
спрямований по дотичній до траєкторії, він називається дотичним, або тангенційним, прискоренням точки. Дотичне прискорення характеризує хуткість зміни модуля вектора швидкості точки
 .
.
Вектори 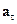 та v збігаються за напрямком при прискореному русі точки; вектори
та v збігаються за напрямком при прискореному русі точки; вектори 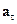 та v взаємно протилежні за напрямком при сповільненому русі точки; і
та v взаємно протилежні за напрямком при сповільненому русі точки; і 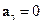 при її рівномірному русі. Якщо
при її рівномірному русі. Якщо 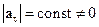 , то рух називається рівнозмінним. При рівнозмінному русі модуль швидкості точки залежить від часу лінійно
, то рух називається рівнозмінним. При рівнозмінному русі модуль швидкості точки залежить від часу лінійно
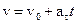 ,
,
де  – модуль початкової швидкості, тобто швидкості в початковий момент часу
– модуль початкової швидкості, тобто швидкості в початковий момент часу 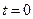 .
.
Складова 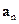 прискорення
прискорення 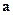 точки називається її нормальним прискоренням. Оскільки вона напрямлена протилежно до радіуса, то її часто називають також доцентровим, або доосередковим прискоренням точки. Величину нормального прискорення можна розрахувати за формулою
точки називається її нормальним прискоренням. Оскільки вона напрямлена протилежно до радіуса, то її часто називають також доцентровим, або доосередковим прискоренням точки. Величину нормального прискорення можна розрахувати за формулою
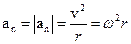 .
.
Нормальне прискорення характеризує хуткість зміни напрямку вектора швидкості точки.
Якщо точка рухається прямолінійно, то нормальне прискорення 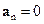 і повне прискорення точки дорівнює її дотичному прискоренню:
і повне прискорення точки дорівнює її дотичному прискоренню: 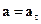 .
.
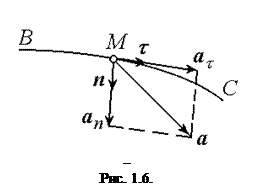
У загальному випадку руху матеріальної точки по криволінійній траєкторії, вектор прискорення точки лежить у дотичній площині, проведеній в розглядуваній точці М траєкторії, і напрямлений у сторону ввігнутості траєкторії ВС (рис. 1.6). У цій же площині лежать і вектори 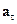 та
та 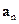 .
.
Дата добавления: 2015-04-07; просмотров: 1749;
