Траєкторія, довжина шляху та вектор переміщення точки

Задачею кінематики є описати рух матеріальної точки без з’ясування його причин. Описати рух матеріальної точки – означає вказати її положення в будь-який момент часу, тобто вказати для кожного моменту часу ту точку системи відліку, де перебуває матеріальна точка. При своєму русі точка проходить неперервну послідовність точок систем відліку. Лінія, яку описує в просторі рухома точка, називається траєкторією цієї точки.

Описати рух матеріальної точки можна в координатній формі. Матеріальна точка, яка вільно рухається в просторі, може здійснювати тільки три незалежних рухи, тобто таких, жоден із яких не можна подати у вигляді комбінації інших. І справді, рух точки вздовж кожної з осей прямокутної декартової системи координат не можна здійснити за рахунок її переміщення вздовж інших двох осей. Число незалежних рухів, які може здійснювати механічна система, називається числом ступенів вільності цієї системи. Отже, матеріальна точка має три ступені вільності, і її положення визначається трьома координатами. При русі ці координати змінюються, тобто є деякими функціями часу. Описати рух – це вказати ці функції. У випадку прямокутної декартової системи координат для опису руху достатньо системи трьох рівнянь:

,

,

.

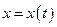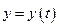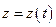Положення тіла можна задати за допомогою радіус-вектора 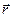відносно деякої точки, яку прийнято за початок відліку. Таке задання положення тіла передбачає лише наявність системи відліку і не потребує введення системи координат. Радіус-вектор розглядається як величина, котра задається для різних моментів часу. Описати рух матеріальної точки у векторній формі означає вказати залежність .

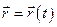Вищезгадані рівняння називаються кінематичними рівняннями руху. Вони задають рівняння траєкторії матеріальної точки в параметричній формі (параметр – час t). Залежно від форми траєкторії, розрізняють прямолінійний і криволінійний рух точки. Рух точки називається плоским, якщо її траєкторія цілком лежить в одній площині.

У загальному випадку траєкторія матеріальної точки являє собою не плоску, а просторову криву. Для такої кривої вводиться поняття стичної площини. Стичною площиною в довільній точці М кривої називається граничне положення площини, яка проходить через будь-які три точки кривої, коли ці точки необмежено наближаються до точки М.

Стичним колом у точці М кривої називається границя кола, яке проходить через три точки розглядуваної кривої, коли ці точки необмежено наближаються до точки М. Стичне коло лежить у стичній площині. Центр стичного кола і його радіус називаються відповідно центром (осередком) кривизни і радіусом кривизни розглядуваної кривої в точці М. Пряма, що з’єднує точку М із центром кривизни, називається головною нормаллю до кривої в точці М. Дотична до кривої в точці М перпендикулярна до головної нормалі в цій точці і також лежить у стичній площині.

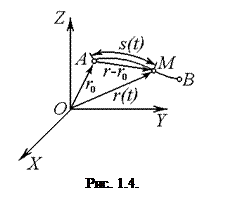
Довжиною шляху точки називається сума довжин усіх ділянок траєкторії, пройдених цією точкою за розглядуваний проміжок часу. Момент часу 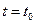, з якого починає розглядатися рух точки, називається початковим моментом часу, а положення точки в цей момент (точка А на рис. 1.4) – початковим положенням. Через довільність вибору початку відліку часу зазвичай покладають t₀ = 0. Довжина шляху s, пройденого точкою з її початкового положення, є скалярною функцією часу: s = s(t), причому, як видно з самого означення, довжина шляху точки не може бути від¢ємною величиною. Якщо точка рухається по дуговій траєкторії АВ (рис. 1.4) весь час в одному напрямку і в момент часу t знаходиться в точці М, то s(t) = ^ÈAM. Якщо ж точка рухається по траєкторії більш складним чином, наприклад на момент часу 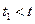переміщується з А в В, а потім, рухаючись у зворотному напрямку, на момент часу t повертається в точку М, то s(t) = ^ÈAB+^ÈBM.

Вектором переміщення точки за проміжок часу від t = t₁ до t = t₂ називається вектор, проведений із положення точки в момент t₁ в її положення в момент t₂. Він дорівнює приросту радіуса-вектора точки за розглядуваний проміжок часу

.

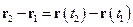Вектор переміщення завжди спрямований уздовж хорди, що стягує відповідну ділянку траєкторії. На рис. 1.4 показано вектор переміщення точки за проміжок часу від t₀ до t , який складає величину r – r₀ = r(t) – r(t₀).

Вектор переміщення точки за проміжок часу від t до t+ 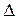t дорівнює

,

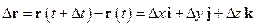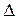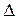де x, y і 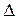z – прирости (зміни) координат точки за розглядуваний проміжок часу.