Система відліку.
В механіці рухом називають зміну положення тіла в просторі з плином часу. При цьому, визначають саме відносне положення, тобто розташування певного тіла відносно інших тіл. Наприклад, є сенс говорити про положення планети відносно Сонця, літака чи теплохода – відносно Землі, але не можна вказати їх положення в просторі “взагалі”, безвідносно до якого-небудь конкретного тіла. Уявне абсолютно тверде тіло, відносно якого визначається положення інших тіл, називається системою відліку. У кожній конкретній задачі вибір системи відліку здійснюється так, щоб якнайбільше спростити розв’язання цієї задачі. Зазвичай у фізиці користуються інерціальними системами відліку.
Для опису простору, в якому здійснюється рух матеріального тіла, з системою відліку пов’язують просторову систему координат. 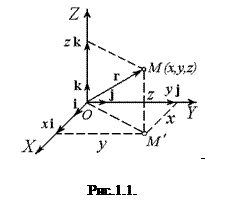 Найбільш поширеною є прямокутна декартова система координат (рис.1.1), ортонормований базис якої утворений трьома одиничними за модулем і взаємно ортогональними векторамиi, j та k, проведеними з початку координат О. Слід підкреслити, що взаємне розташування ортів i, j та k не довільне, а однозначно задається співвідношенням
Найбільш поширеною є прямокутна декартова система координат (рис.1.1), ортонормований базис якої утворений трьома одиничними за модулем і взаємно ортогональними векторамиi, j та k, проведеними з початку координат О. Слід підкреслити, що взаємне розташування ортів i, j та k не довільне, а однозначно задається співвідношенням 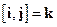 .
.
Положення довільної точки М характеризується радіусом-вектором r, який з’єднує початок координат О з точкою М. Вектор r можна розкласти за базисом 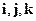 :
:
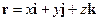 ,
,
де x i, y jта z k– компоненти (складові) вектора r за осями координат. Коефіцієнти розкладу 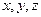 – це декартові координати точки М, а також, внаслідок ортогональності векторів базису, – проекції радіуса-вектора r на відповідні осі координат.
– це декартові координати точки М, а також, внаслідок ортогональності векторів базису, – проекції радіуса-вектора r на відповідні осі координат.
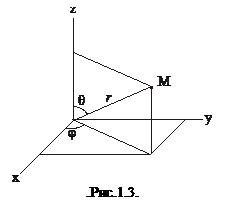
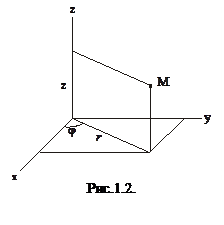 Окрім декартової системи координат, часто вживають циліндричну та сферичну системи координат (див. рис.1.2 та 1.3). У циліндричній системі координатами точки є три числа:
Окрім декартової системи координат, часто вживають циліндричну та сферичну системи координат (див. рис.1.2 та 1.3). У циліндричній системі координатами точки є три числа: 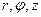 . Як видно з рис.1.2, циліндричні координати можна виразити через декартові координати
. Як видно з рис.1.2, циліндричні координати можна виразити через декартові координати
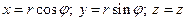 .
.
У сферичній системі координатами є радіус і два кути: 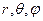 . Перехід від сферичних до декартових координат можна здійснити за формулами
. Перехід від сферичних до декартових координат можна здійснити за формулами
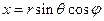 ,
,
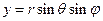 ,
,
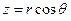 .
.
Очевидно, що фізичний результат розв’язку тієї чи іншої задачі не повинен залежати від вибору системи координат. Вибір системи координат здійснюється дослідником з міркувань зручності розгляду та спрощення математичних перетворень. Одним з найважливіших моментів, що впливає на вибір системи координат, є симетрія задачі. Наприклад, для опису руху об’єкта по поверхні сфери доцільно застосувати сферичну систему координат (можна застосувати і декартову, але математичні викладки вийдуть громіздкими).
 У фізичних задачах часто використовуються математичні вирази для нескінченно малих елементів об’єму
У фізичних задачах часто використовуються математичні вирази для нескінченно малих елементів об’єму 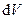 . У декартовій системі координат диференціал об’єму виглядає найпростіше:
. У декартовій системі координат диференціал об’єму виглядає найпростіше: 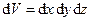 . У циліндричній та сферичній системах диференціали об’єму записують відповідно
. У циліндричній та сферичній системах диференціали об’єму записують відповідно
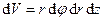 ,
,
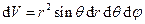 .
.
Наведені вирази отримують з простих геометричних міркувань.
Рух матеріальної точки повністю визначений, якщо задані три неперервні та однозначні функції її координат від часу t, наприклад, 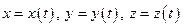 або
або 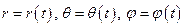 . Ці рівняння називаються кінематичними рівняннями руху точки. Вони еквівалентні одному векторному рівнянню руху точки:
. Ці рівняння називаються кінематичними рівняннями руху точки. Вони еквівалентні одному векторному рівнянню руху точки: 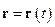 .
.
Дата добавления: 2015-04-07; просмотров: 1140;
