Вращение твердого тела вокруг неподвижной оси, его момент инерции и кинетическая энергия.
Моментом инерциисистемы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
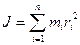 .
.
В случае непрерывного распределения масс эта сумма сводится к интегралу
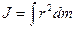 ,
,
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
Если ось, относительно которой вычисляется момент инерции, проходит через центр симметрии тела, то вычисление такого интеграла представляет сравнительно несложную задачу, но в общем случае задачу решить трудно. Для упрощения вычислений полезной оказывается теорема о параллельном переносе осей инерции (теорема Гюйгенса - Штейнера), формулировка которой гласит, что момент инерции относительно любой оси равен сумме момента инерции относительно параллельной оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния d между осями, т.е.
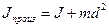 .
.
Моменты инерции некоторых тел:
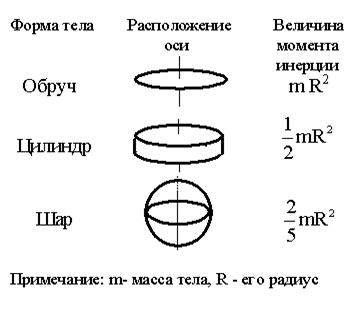
Вычислим кинетическую энергию вращающегося тела. Кинетическая энергия одной частицы вращающегося тела массой 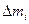 , движущейся со скоростью
, движущейся со скоростью 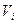 по окружности радиусом
по окружности радиусом 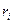 , равна
, равна
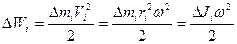 ,
,
где 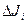 - момент инерции частицы,
- момент инерции частицы, 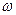 - угловая скорость вращения тела. Тогда энергия вращающегося тела
- угловая скорость вращения тела. Тогда энергия вращающегося тела
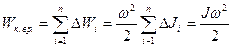 .
.
Дата добавления: 2015-04-15; просмотров: 2948;
