Момент импульса. Закон сохранения момента импульса. Второй закон динамики для вращательного движения.
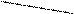 Моментом импульса (количества движения)материальной точки А относительно неподвижной точкиО называется физическая величина, определяемая векторным произведением:
Моментом импульса (количества движения)материальной точки А относительно неподвижной точкиО называется физическая величина, определяемая векторным произведением:
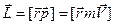 .
.
где 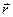 — радиус-вектор, проведенный из точки О в точку A;
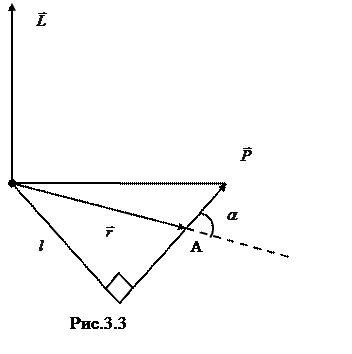
— радиус-вектор, проведенный из точки О в точку A; 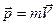 — импульс материальной точки (рис.3.3); Модуль вектора момента импульса
— импульс материальной точки (рис.3.3); Модуль вектора момента импульса
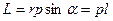
Моментом импульса относительно неподвижной осиz называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса Lz не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса 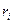 с некоторой скоростью
с некоторой скоростью 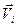 . Скорость и импульс перпендикулярны этому радиусу, т. е. радиус является плечом вектора
. Скорость и импульс перпендикулярны этому радиусу, т. е. радиус является плечом вектора 
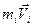 . Поэтому можем записать, что момент импульса отдельной частицы
. Поэтому можем записать, что момент импульса отдельной частицы
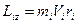
где 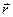 — радиус-вектор, проведенный из точки О в точку A;
— радиус-вектор, проведенный из точки О в точку A; 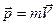 — импульс материальной точки (рис.3.3); Модуль вектора момента импульса
— импульс материальной точки (рис.3.3); Модуль вектора момента импульса
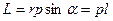
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого телаотносительно оси есть сумма моментов импульса отдельных частиц:
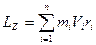
Учитывая, что 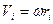 , получим
, получим
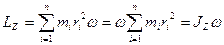 , т. е.
, т. е.
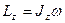
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем последнее уравнение по времени:
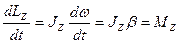 , т.е.
, т.е.
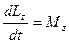
Это выражение — является основным уравнением (законом) динамики вращательного движения твердого телаотносительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Это уравнение можно выразить следующим образом:
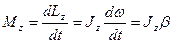 .
.
Если ось z совпадает с главной осью инерции, проходящей через центр масс, то можно написать:
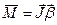 ,
,
т.е. момент силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.
В замкнутой системе момент внешних сил 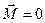 и
и 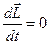
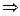
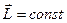 . Данное выражение представляет собой закон сохранения момента импульса:момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
. Данное выражение представляет собой закон сохранения момента импульса:момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Дата добавления: 2015-04-15; просмотров: 1008;
