Уравнение Бернулли и выводы из него
     
  
 |
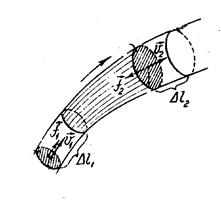Рис.4.3
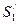и 
. При перемещении изменяется кинетическая и потенциальная энергии выделенного элемента. По закону сохранения энергии величина этого изменения определяется
работой сил давления f1 = p1S1 и f2 = p2S2, которые действуют на плоскости S1 и S2. Как видно из рис., часть элемента между сечениями 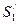и S2 остается неподвижной так, что изменение положения выделенного элемента сводится к перемещению отрезка, ограниченного сечениями S1 и 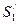в новое положение между плоскостями S2 и . Пусть плотность жидкости в сечении S1 равна r1, а в сечении S2 - r2. Масса отрезка между сечениями S1 и 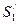равна m1 = r1v1S1Dt, тогда как масса между S2 и равна m2 = r2v2S2Dt; поэтому кинетическая и потенциальная энергии массы m1 равны:
= 
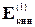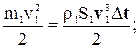
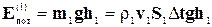. (4-8)
Аналогично для массы m2:
= 
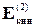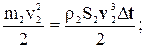
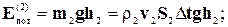(4-9)
где h1 и h2 - высоты центров тяжести первого и второго элементов относительно выбранного уровня отсчета потенциальной энергии.
На основании закона сохранения механической энергии можно записать:
= 
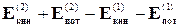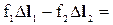
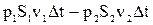. ( 4-10)
Работа силы f2 взята со знаком минус потому, что направление силы и направление перемещения противоположны друг другу.
Подставляя в уравнение (4-10) значения кинетических и потенциальных энергий (4-8) и (4-9), получаем:
= 
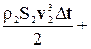
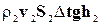
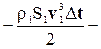
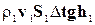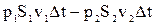, (4-11)
откуда после сокращения на величину Dt (с учетом того, что v1S1 =v2 S2) следует:
= 
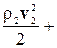
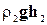
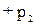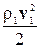
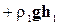
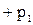,(4-12)
или в общем виде:
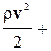
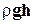+ р = const. (4-13)
Выражения (4-12) и (4-13) представляют различные формы записи уравнения Бернулли, имеющего ряд важных следствий практического характера.Если движение жидкости или газа происходит на постоянной высоте, то уравнение (4-13) упрощается: 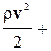р = const, или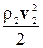 
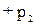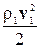
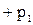= .(4-14 )
Из этого уравнения следует, что давление внутри трубки тока зависит от скорости: там, где скорость меньше, давление больше, при увеличении скорости потокадавление в нем уменьшается. Это утверждение называют принципом Бернулли.
Приложения уравнения Бернулли:подъемной силы крыла самолета, гидротрубина, гидротаран, водоструйный насос, аэрация почвы и т. д.
Дата добавления: 2015-04-15; просмотров: 1062;