Сложение гармонических колебаний.

Наиболее простым примером является сложение двух одинаково направленных гармонических колебаний одинаковой частоты, каждое из которые можно представить в аналитическом виде x₁(t) = A₁sin (wt + j₁) и x₂(t) = A₂ sin (wt + j₂) и векторном виде (рис.5.3).

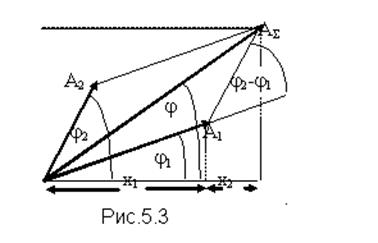
Поскольку оба слагаемых вращаются с одинаковой частотой, суммарный вектор также вращается с этой же частотой, т.е. результатом суммы x₁(t) и x₂(t) будет гармоническое колебание той же частоты, амплитуда которого находится как диагональ параллелограмма А_S, построенного на векторах А₁ и А₂:

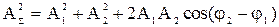; (5-2)

разность j₂-j₁ определяется из рис.5.3. Величина начальной фазы j результирующего колебания определяется из величины тангенса этого угла:

,

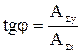где А_Sy и А_Sх представляют собой проекции амплитуды суммарного колебания на оси Y и X соответственно. Как следует из рисунка, значение А_Sх равно сумме проекций на ось Х каждого из слагаемых колебаний:

А_Sх = Х₂ + Х₁ = А₂ cos j₂ + A₁ cos j₁ . (5-3)

Аналогичное выражение может быть получено и для суммарной проекции на ось Y ( для простоты Y - проекции на рис.5.3 не показаны):

А_{S y} = Y₂ + Y₁ = A₂ sin j₂ + A₁ sin j₁ . (5-4)

Тогда

. (5-5)

Таким образом, определены основные параметры суммарного колебания: амплитуда, частота и начальная фаза. Несколько сложнее найти сумму двух колебаний, если их частоты отличаются друг от друга. Практически интересным является случай, когда это различие незначительно, т.е. w₁= w₀ + W и w₂ = w₀ - W, причем W<< w₀ . Пусть для простоты амплитуды обоих колебаний и их начальные фазы одинаковы. Тогда x₁(t) = Asin(w₀ + W)t и x₂(t) = Asin(w₀ - W)t . Суммируя эти выражения, получим

x₁(t)+ x₂(t) = A{sin(w₀ + W)t + sin(w₀ - W)t} = [2AcosWt] sin w₀t, (5-6)

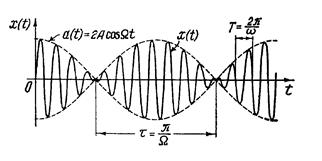Рис.5.4	где величину, стоящую в квадратных скобках, можно рассматривать как медленно меняющуюся амплитуду. Результат суммы таких колебаний, представленный на рис.5.4, называется биениями. Если амплитуды слагаемых колебаний неодинаковы, то картина наблюдающихся биений отличается от
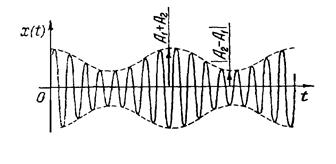Рис.5.5	предыдущей, т.к теперь суммарная амплитуда изменяется от значения А1+А2 до минимума А1-А2. Важно отметить, что в обоих случаях суммарное колебание не является гармоническим, хотя оно и записывается в виде произведения гармонических функций, т.к. его амплитуда не остается постоянной и медленно изменяется с течением времени (рис.5.5).