Уравнение неразрывности.

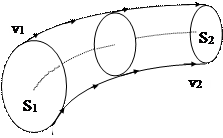
Как уже отмечалось, при стационарном движении жидкости (или газа) скорость ее частиц не изменяется с течением времени. Для наглядности вводится понятие линии тока, которые представляют собой линии, касательные к которым в любой точке совпадают по направлению с вектором скорости в этой же точке. В случае стационарного движения линии тока неподвижны и совпадают с траекториями частиц жидкости. Кроме того, для облегчения изучения движения жидкости вводится понятие трубки тока. Эти трубки образуются так, что линия тока, проходящая через какую-либо точку, лежащую на поверхности трубки тока, целиком лежит на этой поверхности (рис.4.2).

S   Рис. 4.2

При стационарном течении жидкости стенки трубки тока неподвижны. Жидкость, вошедшая в трубку, в дальнейшем движется все время внутри ее. Поэтому выделенную трубку можно рассматривать независимо от остальной жидкости. Предположим, что выделенная трубка тока настолько тонка, что в каждой точке ее поперечного сечения величину скорости частиц жидкости можно

было бы считать одинаковой. Пусть в сечении S₁ (рис.4.2) скорость частиц жидкости равна v₁. За промежуток времени Dt через сечение пройдет объем жидкости V₁=v₁Dt S₁. Если плотность жидкости в этом сечении равна r₁, то через сечение проходит масса m₁=r₁V₁= r₁v₁Dt S₁. Аналогично через сечение S₂ за время Dt проходит масса m₂=r₂v₂Dt S₂. При стационарном движении количество вещества, проходящее через сечения S₁ и S₂ , должно быть одинаковым, т.е. m₁=m₂. Поэтому r₁v₁Dt S₁ = r₂v₂Dt S₂. При несжимаемости жидкости r₁= r₂, откуда следует, что v₁ S₁=v₂ S₂ , или в общем виде

vS = const . (4-7)

Выражение (4-7) носит название уравнения неразрывности. Примером проявления свойств жидкости, описываемых этим уравнением, может служить течение рек: в узких местах скорость течения возрастает и, наоборот, в широких местах скорость течения становится меньше.