Волновое уравнение. Распространение волн в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных

Распространение волн в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (17.2.2), описывающую бегущую волну:

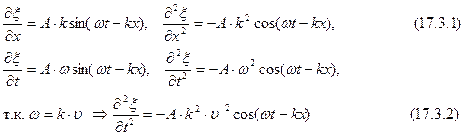
Сравнивая уравнения (17.3.1) и (17.3.2), можно записать

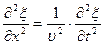
Следовательно, производные по координатам x,y и z

, ,

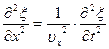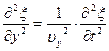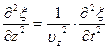
Сложив производные по координатам

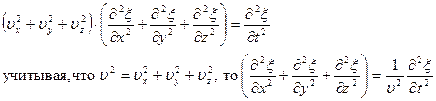
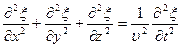- волновое уравнение для плоской волны

Используя, оператор Лапласа

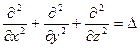
волновое уравнение примет вид

.

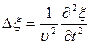Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны).