Волновое уравнение. Если к горной породе приложить внешнюю силу, вызывающую напряжение (взрыв), то, как было показано выше

Если к горной породе приложить внешнюю силу, вызывающую напряжение (взрыв), то, как было показано выше, произойдет деформация, смещение частиц породы на расстояние x в направлении действия силы F(s). Так как частицы пород жестко связаны между собой таким образом, что смещение одной частицы вызывает смещение другой и т.д. (принцип домино), произойдет распространение упругой гармонической деформации с некоторой скоростью. Найдем уравнение возникающих при этом гармонических колебаний частиц. Для простоты ограничимся вначале случаем, когда напряжение действует вдоль одной координаты x. Согласно второму закону Ньютона,

ma=F, (VIII.12)

где а – ускорение, m – масса частицы,

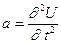. (VIII.13)

Величина U = x характеризует смещение частиц от некоего положения равновесия. Обозначим массу частицы как произведение объема V на плотность r:

m = V·r = DxDyDz·r. (VIII.14)

Перепишем выражение (VIII.13) с учетом (VIII.14) и (VIII.15):

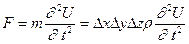. (VIII.15)

Если силы действуют вдоль одной оси x, то сумма всех сил F будет равна сумме напряжений s_x, действующих на соответствующую площадь (объем) S:

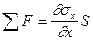, (VIII.16)

где S = DxDyDz.

Подставим (VIII.16) в левую часть уравнения (VIII.15) и после сокращения получим:

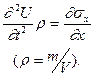(VIII.17)

Теперь воспользуемся законом Гука (VIII.4):

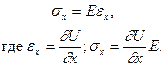(VIII.18)

В итоге получаем волновое уравнение вида:

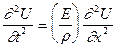. (VIII.19)

Здесь коэффициент 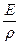есть не что иное, как квадрат скорости распространения продольной волны в породе с_p:

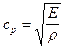, (VIII.20)

или

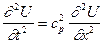. (VIII.21)

Это и есть уравнение распространения упругих гармонических колебаний части среды вдоль координаты x, фронт которых имеет вид плоскости. Отсюда название – уравнение плоских волн.

Для полного определения распространения колебаний необходимо задать начальные и граничные условия. Начальные условия характеризуют состояние колеблющегося источника в начальный момент времени, т.е. при t = 0.

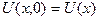– смещение частиц среды,

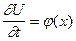– скорость смещения в начальный момент времени t.

Граничные условия показывают характер волнового колебания на границах вдоль оси x, т.е. при x = 0 и x = l:

.

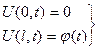Совокупность начальных и граничных условий называется также краевыми условиями. Уравнение (VIII.21) представляет собой линейное дифференциальное уравнение 2-го порядка. Его общее решение имеет вид:

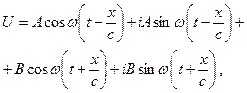(VIII.22)

где A и B – постоянные интегрирования, зависящие от краевых условий. Первые два слагаемых в правой части уравнения (VIII.22) выражают плоскую волну, распространяющуюся в положительном направлении оси x, вторые два выражают обратную, т.е. отраженную от границы l, волну, возвращающуюся к источнику (рис. 58). В безграничной среде отраженной волны не будет, т.е. уравнение примет вид:

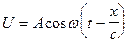, (VIII.23)

где А характеризует амплитуду смещения U в точке x = 0, т.е. амплитуду источника возбуждения. Колебания частиц среды вдоль оси x создаются движением бесконечной плоскости, перпендикулярной направлению распространения волны.

Рис. 58. Образование прямой и отраженной волн в океане:

U^I₁ – отраженная от дна; U₂ – отраженная от поверхности акустического

фундамента; U^II₁ – двухкратно отраженная от дна волна