Связь гравитационного и магнитного потенциалов

Представляет интерес сопоставить гравитационные и магнитные поля, создаваемые одними и теми же геологическими объектами, и выяснить имеется ли между ними какая-либо связь.

Сопоставим между собой гравитационный (V) и магнитный потенциалы (U):

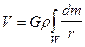; (VII.54)

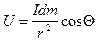. (VII.55)

Дифференцируя (VII.54), получим:

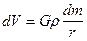, (VII.56)

откуда:

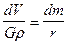. (VII.57)

Из выражения (VII.55) имеем:

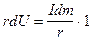(VII.58)

(так как cosQ = 1 при Q = 0, считаем намагниченность пород вертикальной, т.е. приведенной к магнитному полюсу). Здесь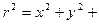

+ z².

Найдем частные производные от правой части выражения (VII.57):

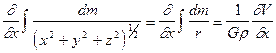; (VII.59)

(так как 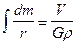, что следует из (VII.54)).

Далее:

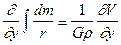; (VII.60)

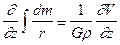. (VII.61)

Подставим (VII.59, VII.60, VII.61) в (VII.58):

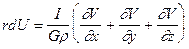. (VII.59)

Введем единичный вектор 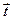, совпадающий с вектором намагниченности ,

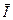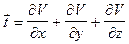. (VII.62)

Тогда выражение (VII.59) можно переписать в виде:

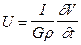. (VII.63)

Это выражение называется уравнением Пуассона. Оно устанавливает связь между гравитационным и магнитным потенциалами. В частности, из соотношения (VII.63) следует, что магнитный потенциал равен произведению гравитационного потенциала, умноженного на коэффициент 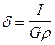, который для каждой данной аномалии будет величиной постоянной, т.е.

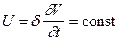. (VII.64)