Интерпретация магнитных аномалий

Анализируя полученные в предыдущем параграфе формулы для Dz, DH и V и соответствующие им графики, нетрудно увидеть, что тела различной формы нередко создают весьма сходные магнитные аномалии. Это обусловливает неоднозначность количественных решений обратной задачи магнитометрии в целом и геологической интерпретации магнитных наблюдений в частности. Тем не менее в ряде случаев удается оценить размеры и глубину залегания верхней, а иногда и нижней кромки магнитовозмущающих тел. При этом для упрощения вычислений приходится чаще всего исходить из предположения о вертикальном намагничении тел.

Определение элементов залегания вертикального стержня бесконечной длины. Изометрические аномалии Dz и DT одного знака (см. рис. 46, с. 183) являются указанием на то, что глубина залегания нижнего края намагниченного тела весьма значительна, а поперечные размеры тела примерно соответствуют размерам и конфигурации изодианам или изолиний DT. Для интерпретации таких аномалий можно использовать формулы для вертикального стержня бесконечной длины:

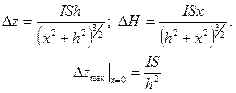(VII.36)

Откуда легко определить глубину до верхней кромки:

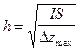. (VII.37)

Так как величина IS обычно неизвестна, то удобнее пользоваться другой формулой:

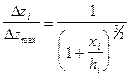, (VII.38)

где Dz_i – текущее значение кривой Dz на пикетах профиля.

Для отношения (VII.38) можно рассчитать таблицы, из которых легко определить x_i/h.

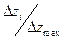
	0,8	0,5	0,25
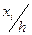
	0,4	0,75	1,2

Например, на абсциссе x_1/2, где величина

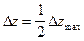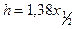, . (VII.39)

По полученным таким образом значениям h и Dz_max можно оценить величину 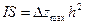. Если же интенсивность намагничивания I известна, например, по определениям на образцах ( 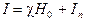), то можно вычислить площадь верхней кромки намагниченного тела:

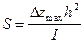. (VII.40)

Определение элементов залегания намагниченного шара. Интенсивная положительная изотермическая аномалия, вокруг которой располагается слабая отрицательная аномалия (см. рис. 47 на с. 184), свидетельствует о том, что нижняя кромка намагниченного тела залегает на сравнительно небольшой глубине. Для интерпретации таких аномалий можно использовать формулы для шара:

; .

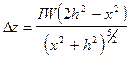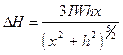При x = 0 получаем 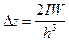, откуда нетрудно определить глубину над центром шара:

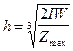. (VII.41)

При известном I можно оценить радиус шара и примерный объем намагниченного тела:

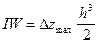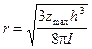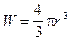; ; . (VII.42)

Определение элементов залегания тонкого пласта бесконечной длины. Вытянутые аномалии одного знака свидетельствуют о большой глубине залегания нижней кромки намагниченного тела, форма которого, очевидно, близка к вертикальному пласту бесконечного простирания (см. рис. 48 на с. 185). Для Dz и DH имеем выражение:

; ,

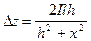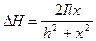Решая оба уравнения относительно h, получим:

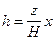. (VII.43)

Произвольно беря x_i и соответствующие им значения Dz_i и DH_i, легко определяем глубину залегания верхней кромки пласта. Если кривые Dz и DH были действительно обусловлены такой формой тела, то все h, рассчитанные в нескольких точках профиля x, совпадут с небольшим разбросом. В противном случае этот разброс будет велик.

Интерпретацию можно производить также, пользуясь лишь кривой Dz. Решая совместно два уравнения, полученные для Dz_max и любого текущего значения Dz_i

, ;

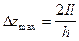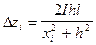получим:

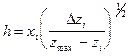. (VII.44)

В точке профиля, где 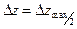, h = x_1/2, т.е. абсциссе этой точки. Если по образцам или каким-либо иным способом определена интенсивность намагничивания I, то по полученным значениям h и I можно оценить ширину намагниченного тела:

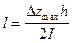. (VII.45)

Зная Dz и h, легко определить намагниченность:

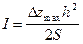. (VII.46)

Графические способы интерпретации. В отличие от рассмотренных выше аналитических способов определения параметров геологического объекта, где для расчетов используются лишь отдельные экстремальные значения аномалий, в графических способах реализуется большая часть аномальной кривой Dz, DH или DT. Это повышает точность интерпретации, что с учетом относительной простоты операций вычисления h делает графические способы предпочтительнее аналитическим.

Одним из таких способов является так называемый способ касательных, реализующий в первом приближении связь ширины аномалии с глубиной залегания намагниченного тела. В первоначальном варианте, предложенном Ю. И. Грачевым, определение глубины залегания верхней кромки магнитовозмущающих тел проводилось следующим образом:

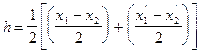. (VII.47)

Значения x₁, x₂, xґ₁ и xґ₂ видны из рис. 52.

Эта формула дает весьма приблизительную оценку h для тел, близких к вертикальному пласту большой мощности (l ³ 2h), нижняя кромка которого не оказывает влияние на величину потенциала V.

В общем виде формула Грачева имеет вид:

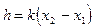, (VII.48)

где k – коэффициент, зависящий от формы тела. У Грачева k = 1, однако дальнейшие исследования показали, что для различных форм намагниченных тел коэффициент k сильно различается:

– для монополя k = 0,859;

– для цилиндра k = 0,650;

– для уступа k = 0,318 и т.д.

Формула (VII.48) получается из выражения (Гладкий, 1967):

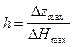, (VII.49)

где DH_max находится при помощи касательной (рис. 53).

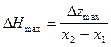. (VII.50)

Подставляя это значение в равенство (VII.49), получим (VII.48).

Более точный вариант способа касательных разработан В. К. Пятницким, показавшим необходимость учета изменения мощности и глубины кромки.

В способе Пятницкого аномалия аппроксимируется пятью касательными. Проекции отрезков ломаной линии касательных на ось x и xґ связаны с глубиной и относительной мощностью магнитовозмущающих тел следующими соотношениями:

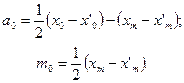(VII.51)

Вычисление глубины h и средней намагниченности I_ср. производится по формулам:

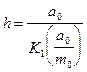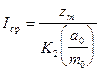; . (VII.52)

Коэффициенты K₁ и K₂ находятся из таблицы, рассчитанной для идеальных аномалий.

Таблица VII.1