Отражение волн на границе вода – дно

Эта чрезвычайно важная задача позволяет понять физику процесса формирования звукового поля выше и ниже границы раздела вода-дно в океане. Впервые она была решена в полной мере для продольных и поперечных волн Л. М. Бреховским (1957). Здесь мы дадим упрощенное решение этой задачи.

Рассмотрим случай, когда образование поперечной волны в морском грунте не происходит. С физической точки зрения такая задача соответствует отражению волны от границы двух жидких сред. В первом приближении такой подход дает удовлетворительное решение для оценки условий формирования отражений на границе вода-дно и одновременно упрощает анализ.

Предположим, что источник колебаний (взрыв) находится в водном слое, откуда прямая волна U, падая на границу z, разделяющую две среды с разным акустическим импедансом – r₁с₁ и r₂с₂, образует отраженную волну U₂ и проходящую под дно (преломленную) волну U₃ (рис. 59). Представим волны U₁, U₂, U₃ в виде составляющих вектора К по осям координат x, z (плоская задача). Вектор K будет перпендикулярен поверхности волнового фронта и определяет направление луча: ; ,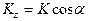

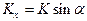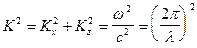. (VIII.49)

С учетом этого решение волнового уравнения для падающей U₁, отраженной U₂ и преломленной волн U₃ будет иметь вид:

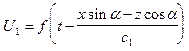, (VIII.50)

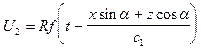, (VIII.51)

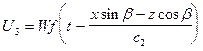. (VIII.52)

Здесь R – коэффициент отражения от дна, W – коэффициент преломления; a, b – углы падения, отражения и преломления; c₁,c₂ – скорость звука выше и ниже границы раздела (дна моря).

Выберем начало координат на границе, т.е. z = 0. Так как среда непрерывна, то нормальные смещения на границе U₁, U₂ и U₃ также непрерывны и равны

U₁ + U₂ = U₃. (VIII.53)

Давление P также должно быть равно по обе стороны от границы, так как в противном случае среда на границе z = 0 будет терпеть разрыв и волна в пространство r₂с₂ не пройдет. Так как

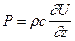, (VIII.54)

то равенство давлений можно записать так:

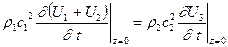. (VIII.55)

Горизонтальные смещения равны нулю, т.е. мы предполагаем среды по обе стороны границы жидкими:

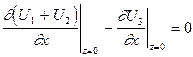. (VIII.56)

С учетом (VIII.50, VIII.51, VIII.52) полное звуковое поле на границе вода-дно будет иметь вид:

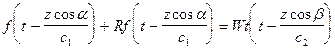. (VIII.57)

Продифференцируем обе части выражения (VIII.57) согласно граничному условию (VIII.55):

;

.

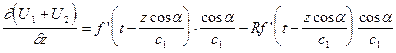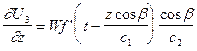С учетом (VIII.55) получим:

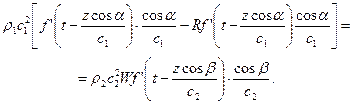(VIII.58)

Поскольку имеет место соотношение Снеллиуса:

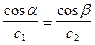, (VIII.59)

то подставим его в уравнения (VIII.57) и (VIII.58) с учетом граничных условий (VIII.55). Можно сократить в (VIII.57) обе части уравнения на 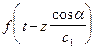, а в уравнении (VIII.58) – на .

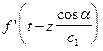В результате получим систему двух уравнений с двумя неизвестными R и W:

,

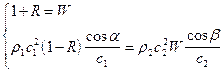или

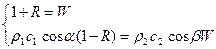. (VIII.60)

Подставим первое уравнение во второе

.

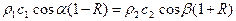Решая его относительно R, получим:

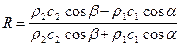. (VIII.61)

Аналогично находим W:

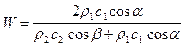. (VIII.62)

Полученные уравнения позволяют определять коэффициенты отражения и преломления от границы вода-дно при любых углах падения. Они показывают, что эти коэффициенты зависят от акустических импедансов среды по обе стороны границы и углов падения и преломления.

Для случая нормального падения волны на границу раздела, когда , получим известные формулы Рэлея:

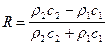; (VIII.63)

. (VIII.64)

Проанализируем полученные выражения для коэффициентов отражения и преломления в случае нормального падения волны на границу раздела.

Перепишем выражение (VIII.63) в виде:

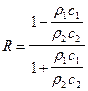. (VIII.65)

Как видно из (VIII.65), коэффициент отражения R от дна обращается в нуль при равенстве акустических жесткостей 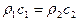в средах по обе стороны от границы z = 0. Если акустическая жесткость r₂с₂ в нижней среде много выше r₁с₁, то R = 1, т.е.

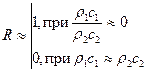. (VIII.66)

Коэффициент преломления при аналогичных условиях приобретает следующие значения:

.

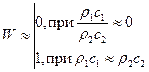Первое условие для r₁с₁ » 0 в реальных средах не имеет смысла, так как морская вода характеризуется конечными вещественными значениями r₁ и c₁ (r₁ » 1,03 г/см³, с » 1500 м/с). Это условие может быть в первом приближении реализовано, если r₁с₁ << r₂с₂. Проведенный анализ показывает, что при равенстве акустических жесткостей воды и пород дна (что может иметь место в случае рыхлого, водонасыщенного грунта) коэффициент преломления равен:

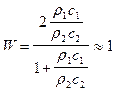, (VIII.67)

а коэффициент отражения равен нулю, т.е. отражения от такого грунта не будет совсем. Однако коэффициент преломления, как это видно из (VIII.67), в этом случае равен единице, т.е. волна полностью, без искажений и потерь пройдет в грунт, как если бы никакой границы не было. Коэффициент отражения R приобретает максимальное значение, равное единице, в случае резкого перепада акустических жесткостей на границе раздела вода-дно. Это имеет место, если последнее сложено весьма плотными породами – гранитами, базальтами и др. Аналогичный резкий перепад r₀c₀/r₁c₁ происходит на свободной поверхности моря.

Приведем два примера. Акустические сопротивления морской воды и воздуха равны соответственно r₁c₁ = 1,0× 1,5× 10⁶ ; r₀c₀ = 429. Коэффициент отражения на границе воздух-вода при падении из воды в воздух равен:

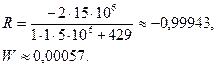
Следовательно, 99% энергии падающей волны отражается от поверхности моря с обратным знаком, т.е. поверхность моря является практически зеркальным отражателем акустической энергии. Поэтому звуки в воде практически не слышны над морем. Для границы вода-базальт получаем: r₁c₁ = 1,5× 10⁶, r₂c₂ = 3,0× 6,5× 10⁶; R = 0,86, т.е. примерно 5/6 падающей на границу энергии волны отражается, и лишь 1/6 проходит в грунт. Этот факт хорошо известен в морской сейсмоакустике и эхолотировании. Плотные грунты всегда дают более четкую запись отражений, чем мягкие осадочные грунты (рис. 60).

Коэффициент отражения меняет знак на обратный, если величина 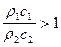, т.е. r₁c₁>r₂c₂. Перемена знака происходит при падении волны из среды с большим акустическим сопротивлением в среду с меньшим акустическим сопротивлением. Это, в частности, имеет место при отражении от свободной поверхности моря, при подходе волны снизу.