Отражение звука от слоя

Рассмотрим задачу об отражении плоской волны от однородного слоя толщиной h, падающей под горизонтальным углом a_i на верхнюю и нижнюю границу слоя (рис. 61). Будем полагать, что среды 1 и 3, разделяемые слоем h, также являются однородными, т.е. распределение скорости и плотности в них по z и по x постоянны. Решение задачи впервые было изложено в работе Л. М. Бреховских (1957). Им мы и воспользуемся.

Эта задача имеет важное приложение для сейсмоакустики и гидроакустики. В частности, таким слоем можно аппроксимировать толщу океанических осадков, подстилаемых базальтовым фундаментом, что справедливо для волн низкой частоты, соизмеримых с мощностью осадочной толщи, либо с каким-нибудь верхним слоем осадков, например, до первой отражающей границы (гори­зонт А). Мощность этого неконсолидированного слоя в океане в среднем меняется в пределах 150 – 300 м.

При прохождении волны через слой происходит интерференция (сложение) колебаний от верхней и нижней границ слоя. Поэтому для результирующего акустического поля в слое h можно написать следующее выражение:

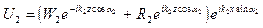. (VIII.68)

Ранее было показано, что отношение акустического давления к колебательной скорости при нормальном падении плоской волны на границу раздела двух сред характеризует волновое сопротивление (импеданс) среды (rc). При произвольном падении a

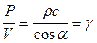. (VIII.69)

Здесь мы обозначим акустический импеданс буквой g, чтобы не путать с координатой z.

При смене направления распространения волны cosa меняет знак и

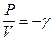. (VIII.70)

В соответствии с этим будем считать, что среды 1, 2, 3 (рис. 61) характеризуются импедансом:

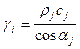, где j=1, 2, 3... (VIII.71)

Найдем акустическое давление и колебательную скорость, создаваемые результирующим полем U₂ в слое h (Бреховских, 1957):

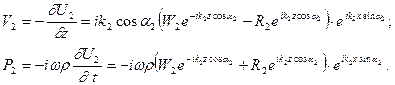(VIII.72)

В соответствии с формулой (VIII.69) отношение 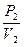на границе z=0 должно равняться импедансу среды 1, т.е.

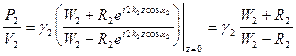, (VIII.73)

откуда

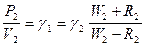, или 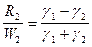. (VIII.74)

На верхней границе слоя, т.е. при z = h, из выражений (VIII.72) имеем:

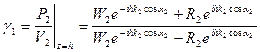, (VIII.75)

Подставляя в (VIII.75) значение 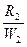из (VIII.74) после простых преобразований с учетом формулы Эйлера:

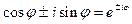, (VIII.76)

получим:

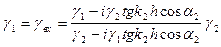. (VIII.77)

Здесь через g_вх мы обозначим входной импеданс на верхней границе слоя. Теперь найдем звуковое поле в среде 3. Соответствующие выражения для давления и колебательной скорости имеют вид:

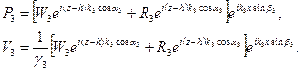(VIII.78)

При z=h отношение 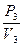должно быть равно входному импедансу слоя g₃, т.е.

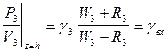. (VIII.79)

Следовательно, коэффициент отражения на верхней границе будет равен:

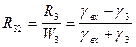. (VIII.80)

Подставляя сюда выражение (VIII.77), для g_вх получим:

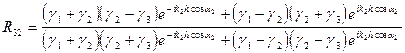. (VIII.81)

Это и есть выражение для коэффициента отражения от слоя толщиной h.

Определим теперь амплитуду прошедшей через слой h волны. Поле этой волны в среде 1 будет:

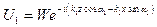. (VIII.82)

Согласно условиям непрерывности смещений, давлений и скорости на границе раздела z=0, смещение U₁ должно быть равно смещению U₂, определенному выражением (VIII.68):

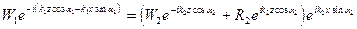. (VIII.83)

Полагая z=0 и учитывая закон Снеллиуса 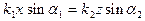, получаем:

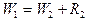. (VIII.84)

Аналогично из условий непрерывности U на границе z=h, согласно выражениям (VIII.68) и (VIII.78), получаем:

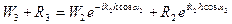
или, с учетом ,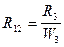

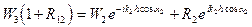. (VIII.85)

Разделим (VIII.84) на (VIII.85) и в полученное выражение подставим значения R₁₂ и :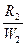

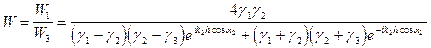. (VIII.86)

Полученная формула характеризует коэффициент прозрачности слоя.

Проанализируем теперь полученные выражения для R₃₂ и W. Если слой имеет нулевую мощность (h = 0), то формулы (VIII.81) и (VIII.86) переходят в обычные выражения для коэффициента отражения и преломления от границы полупространства:

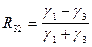; (VIII.87)

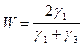. (VIII.88)

Полагая

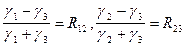(VIII.89)

и подставляя их в формулы (VIII.81) и (VIII.86), получим обобщенные выражения для коэффициента отражения и прозрачности слоя h:

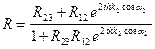, (VIII.90)

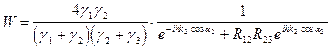. (VIII.91)

Если волна падает вертикально на поверхность слоя, что соответствует случаю глубокого моря, то, полагая в формуле (VIII.81) cosa₂ = 1 и заменив экспоненциальные множители согласно формуле Эйлера 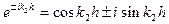, после простых преобразований получим:

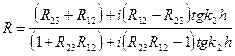. (VIII.92)

Разделив R на действительные и мнимые члены, получим для квадратного модуля 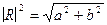, где a=Re(R), b=Im(R); окончательно получим выражение для коэффициента отражения от слоя при нормальном падении волны:

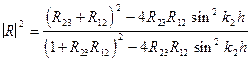. (VIII.93)

Наличие в выражении для 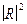функции sin²k₂h свидетельствует, что модуль коэффициента отражения от слоя есть периодическая функция. Максимумы и минимумы осцилляции 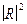легко находятся обычным путем:

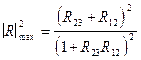, (VIII.94)

что имеет место при sin²k₂h=0, т.е. если k₂h=np, откуда 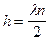; (n=0,1,2...);

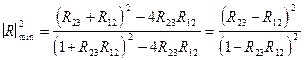, (VIII.95)

что имеет место при sin²k₂h=1, т.е. если 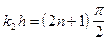, откуда 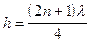. Таким образом, если g₃ < g₂ < g₁, то R₂₃R₁₂ > 0 и коэффициент отражения имеет максимум при отражении от слоя, толщина которого h кратна целому числу полуволн, и минимум, если толщина слоя кратна нечетному числу четверти длины волны. В первом случае

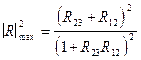; (VIII.96)

во втором

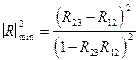. (VIII.97)

Из последнего выражения видно, что если R₂₃=R₁₂, то отражение от слоя будет отсутствовать совсем. Подставляя в это равенство выражение для импедансов сред:

,

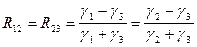получим

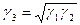. (VIII.98)

Таким образом, если между двумя любыми средами поместить четвертьволновой слой с импедансом, равным среднему геометрическому импедансу этих сред, то отражение от слоя будет отсутствовать совсем.

Можно показать, что коэффициент отражения от слоя с поглощением представляет собой по-прежнему осциллирующую функцию. Однако размах осцилляции уменьшается с увеличением мощности слоя h, и при больших h величина 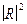становится постоянной величиной, равной модулю коэффициента отражения от верхней границы слоя. Это значит, что в толстом слое с поглощением волны затухают, не доходя до нижней границы слоя и, следовательно, не образуют интерференцию с отраженной от этой границы волной.

Период осцилляции 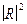тот же, что и в слое без поглощения, с той лишь разницей, что амплитуда осцилляции затухает с увеличением мощности слоя. Следует отметить, что аналогичный эффект поглощения в слое обеспечивается умножением модуля R на экспоненту, учитывающую фактор поглощения a:

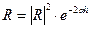. (VIII.99)

Исследование поведения коэффициентов отражения в функции h или частоты w в слоях позволяет определить важнейшие характеристики среды – такие, как скорость звука и поглощение в глубоководных осадочных слоях, что было найдено нами (Орлёнок, 1977; см. §7).