Скорость сферической волны

Колебательная скорость и акустическое давление сферической волны определяются так же, как и для плоской волны.

Найдем колебательную скорость прямой волны:

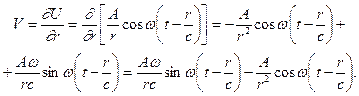(VIII.40)

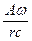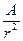Полученное выражение показывает, что амплитуда колебательной скорости в сферической волне в отличие от плоской волны имеет две составляющие – и , первая из которых убывает обратно пропорционально расстоянию r, вторая – квадрату расстояния r². Отсюда следует, что на расстояниях r, больших по сравнению с длиной волны l, второе слагаемое становится малым по сравнению с первым; им можно пренебречь:

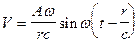. (VIII.41)

Акустическое давление сферической волны определяется из выражения

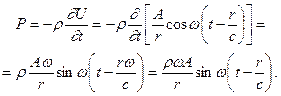(VIII.42)

Для случая r>>l отношение акустического давления к колебательной скорости равно:

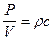, (VIII.43)

т.е. вдали от источника акустическое сопротивление сферической волны равно акустическому сопротивлению плоской волны.

Следовательно, для больших расстояний от источника, равных десяти длинам волн, сферичностью фронтов можно пренебречь и рассматривать сферические волны как плоские.

Интенсивность сферической волны вдали от источника определяется из выражения:

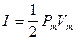, (VIII.44)

где P_m и V_m – амплитуды акустического давления и колебательной скорости прямой сферической волны вдали от источника. Из (VIII.41) и (VIII.42) видно, что

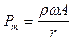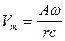; (VIII.45)

или

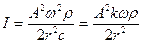. (VIII.46)

Таким образом, интенсивность сферической волны в однородной непоглощающей среде убывает обратно пропорционально квадрату расстояния от источника. С физической стороны это соответствует увеличению волновой поверхности при удалении от источника.

Мощность, переносимая сферической волной вдали от источника, определяется как произведение интенсивности на сферическую поверхность S:

W=IS, (VIII.47)

так как 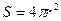, , 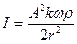, 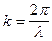то

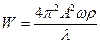. (VIII.48)

Следовательно, мощность излучения пропорциональна квадрату амплитуды и обратно пропорциональна длине излучаемой волны.