Условия применимости лучевого приближения

Рассмотренные выше основы волновой теории распространения упругих колебаний в земной коре дают полную и точную картину формирования сейсмических полей в слоистых средах. Однако, используя только эту теорию, трудно, а часто и просто невозможно получить сведения о кинематике волн, т.е. о временах их пробега и скоростях распространения в различных слоях. Существует тесная зависимость скорости от плотности и, следовательно, от литологии горных пород.

Получить эти параметры можно, используя принципы геометрической сейсмики, т.е. лучевое приближение. Согласно принципу Гюйгенса, траектории лучей всюду перпендикулярны к фронту волны. Следовательно, в однородной среде эти лучи будут представлять собой прямые линии, в неоднородной среде они будут искривлены. Согласно принципу Ферма, волны распространяются вдоль траекторий, требующих наименьшего времени для их прохождения. Этим объясняется прямолинейность траекторий лучей в однородных изотропных средах и их искривление в неоднородных средах.

Применение лучевого приближения в сейсмометрии возможно лишь при соблюдении следующих условий.

1. Радиус кривизны лучей не должен быть больше длины волны.

2. Коэффициенты отражения и преломления существенно не меняются в пределах длины волны.

3. Изменение амплитуды сигнала и условий на границах раздела слоев должно быть мало в пределах длины волны.

4. Линейные размеры неровностей границ сред (шероховатость границы) должны быть меньше длины волны.

В практике сейсмометрии, имеющей дело с инфразвуковыми частотами 10 – 100 Гц, оперируют обычно большими длинами волн, исчисляемыми десятками и сотнями метров, в сравнении с которыми встречающиеся обычно размеры неоднородностей на границах оказываются значительно меньше длин волн. На высоких звуковых частотах соблюдение указанных условий значительно затруднено. Однако и здесь принципы лучевой теории находят применение.

Отражение и преломление лучей на границах раздела подчиняются следующим основным законам.

1. Угол падения равен углу отражения.

2. Угол падения волны a и ее скорость в верхней среде с₁ пропорциональны углу преломления b и скорости волны в нижележащей среде с₂:

.

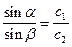Используя принципы геометрической сейсмики, можно получать графики зависимости времени прихода волн, отраженных или преломленных на различных границах раздела внутри земной коры, от расстояния, отсчитываемого от пункта взрыва:

t = f(x)

и по ним рассчитывать скорости этих волн. Такие графики (см. рис. 62) называются годографами. В зависимости от типа волн годографы называются годографами прямых, отраженных, преломленных, рефрагированных или головных волн. Их изучению и посвящены следующие параграфы настоящей главы.