Годограф преломленной волны для многослойной среды

Обращаясь снова к рис. 64, нетрудно видеть, что полное время луча, преломленного на границе 1,2, равно

.

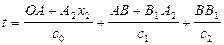Пользуясь рис. 64, найдем координаты начальной точки годографа t₂ и x₂:

(IX.25)

Найдем значение текущей координаты t, т.е. годограф волны, преломленной во втором слое под осадками:

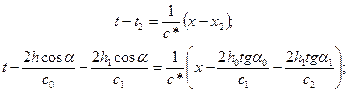(IX.26)

откуда имеем:

;

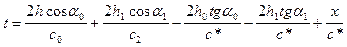После несложных преобразований с учетом 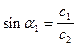, получим

. (IX.27)

Это есть уравнение годографа головной волны, преломленной на второй границе. Следуя модели, приведенной на рис. 64, нетрудно выписать годографы головной волны для трехслойной и n-слойной моделей коры:

, (IX.28)

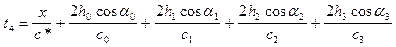. (IX.29)

В общем случае для границы, содержащей n слоев, годограф головной волны имеет вид:

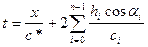. (IX.30)