Годограф преломленной волны

Рассмотрим образование преломленных волн на примере океанского разреза земной коры.

В случае мягкого грунта (R₁ = 0,1-0,3) и безградиентного слоя воды возможно образование преломленной и рефрагированной волн (рис. 64). Тогда согласно закону преломления,

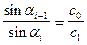(IX.13)

и в предельном случае заворота луча, когда 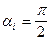, имеем:

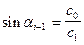, (IX.14)

или

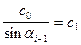. (IX.15)

Выражение 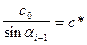называется кажущейся скоростью и характеризует скорость распространения фронта волны вдоль поверхности дна. Следовательно,

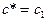, (IX.16)

т.е. кажущаяся скорость в точке выхода луча на поверхность дна должна быть равна скорости в вершине заворота (рефракции) луча под дном моря.

Однако это условие выполняется лишь в консолидированной части разреза, так как скорость в воде не может быть выше предельного для каждого района океана значения, обусловленного температурой, соленостью и гидростатическим давлением. Поэтому кажущаяся скорость прямой (водной) волны, распространяющейся вдоль поверхности воды, будет постоянна.

Как было показано выше, условием образования головной преломленной волны является равенство: 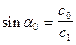; для границы вода-дно и, соответственно, для границ в консолидированной коре:

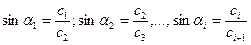(IX.17)

Как видно из рис. 64 первая точка профиля x, в которую приходит преломленная волна, будет x₁. Во все последующие точки профиля лучи преломленной волны подойдут под одним углом e вследствие постоянства параметров водного слоя вдоль горизонтального направления. Следовательно, кажущаяся скорость c* будет постоянна:

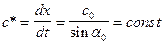. (IX.18)

Отсюда годограф преломленной волны будет прямой линией, начинающейся в точке с координатами x₁ и t₁, и наклонен под углом:

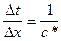, (IX.19)

т.е. величина наклона годографа обратно пропорциональна кажущейся скорости c*.

Найдем координаты начальной точки годографа головной волны x₁ и t₁:

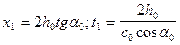. (IX.20)

Теперь определим текущую координату t на произвольном участке профиля x, помня, что, согласно (IX.19), 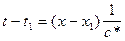. Подставим сюда значения (IX.20): 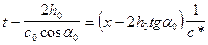, откуда

.

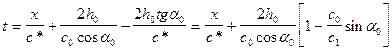Так как 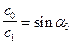, , 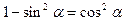то окончательно имеем:

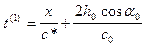. (IX.21)

Это и есть уравнение годографа преломленной на первой границе вода-дно волны.

В точке x = 0 имеем:

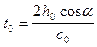, (IX.22)

откуда

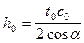. (IX.23)

Для наклонной границы вода-дно:

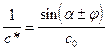, (IX.24)

где знак (–) – по восстанию границы, знак (+) – по падению. Отсюда ясно, что пренебрежение наклоном границы раздела приводит к завышению кажущейся, а с нею и граничной скорости c₁, в случае падения границы и занижению с* и с₁ в случае восстания границы.