Волновое уравнение. Функция - решение этого уравнения.

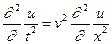(11.1)

Функция 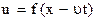- решение этого уравнения.

ξ=x-vt

;

;

;

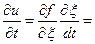
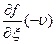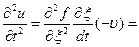
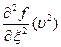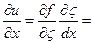
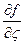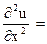
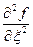
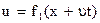- тоже является решением.

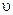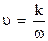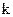- скорость фронта волны. , где - волновое число. ;

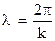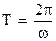
За время от t =0 до произвольного момента времени t график функции смещается на расстояние х = vt. При этом скорость смещения равна v. Говорят, что функция (11.2) опи­сывает волну, бегущую вдоль оси х. Функция (11.3) также описывает бегущую волну. Только эта волна "бежит" в другую сторону, так как график функции (11.3) при увеличении t смещается влево. Величину v называют скоростью распространения волны.

Общее решение уравнения (11.1) имеет вид

u(t, х) =f(x -vt) + h(x + v t),

Рис. 11.1. Бегущая волна

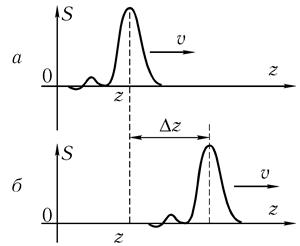
т.е. в общем случае вдоль оси х могут распространяться сразу две волны, одна из которых "бежит" вправо, а другая - влево.