Гармоническая волна

Волна называется гармонической, если она описывается функцией,

ψ(t,х) = А cos(ωt-kx + a), (11.4)

где А - амплитуда волны; ω - частота; к - волновое число; а - начальная фаза;

φ(t, x) =ωt-kx + a (11.5)

- фаза волны. Функцию (11.4) можно привести к виду (11.2):

ψ(t,х) = А cos(-k(x –ωt/k) + a),

видно, что скорость гармонической волны связана с частотой и волновым числом соотношением

v= ω/k (11.6)

Для того чтобы получить зависимость величины ψ от времени t, кото­рая описывает ее изменения со временем в данной точке пространства, следует положить в формуле (11.4) х = const. Так как функция (11.4) при х = const описывает гармонические колебания, говорят, что гармони­ческая волна создает в произвольной точке пространства гармонические колебания.

Величина

T=2π/ω - период волны, а (11.7)

λ=2π/k (11.8)

- длиной волны. Если фаза (11.5) волны получит приращение 2π, то, значение функции (11.4) останется прежним. Поэтому при х= const функция (11.4) принимает одно и то же значение для всех моментов вре­мени, которые отличаются одно от другого на пТ, где п - целое число; а при t = const значения функции (11.4) в различных точках пространства совпадают, если координаты этих точек отличаются друг от друга на пλ. График зависимости величины ψ(t,х) от координаты х при t = const для случая, когда вдоль оси х распространяется гармоническая волна, пока­зан на рис. 11.2.

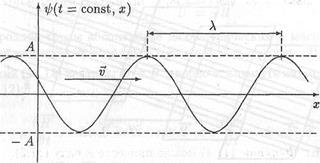
Рис. 11.2. Гармоническая волна

11.3. Волны впространстве

Пусть физическая величина ψ распределена в пространстве, и это рас­пределение меняется со временем. Говорят, что функция ψ = ψ(t,r) описывает волну, распространяющуюся в пространстве, если она удо­влетворяет уравнению

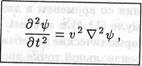
∆- оператор Лапласа.

Волна называется плоской, если существует такая система декартовых координат, в которой функция ψ зависит только от одной из координат. Если этой координатой является х, то уравнение (11.9) сводится к (11.1). В произвольной прямоугольной системе декартовых координат плоская гармоническая волна описывается функцией

ψ(t,r) = A cos(ωt-kr + a), (11.10

где вектор кназывается волновым. В том, что эта функция является решением уравнения (11.9), нетрудно убедиться непосредственной под­становкой.

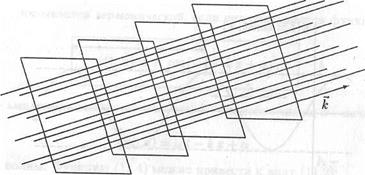
Рис. 11.3. Фазовые поверхности и лучи, вдоль которых распространяется в пространстве плоская волна

Функция

φ(t, r) = ωt –kr+a

называется фазой плоской волны. Поверхность

φ(t = const, r) = const, или kr= const

постоянной фазы (11.11) является плоскостью, к которой вектор кпер­пендикулярен. Такие поверхности называют фазовыми, или волновыми, а линии, перпендикулярные к фазовым поверхностям, называют лучами. Для плоской волны лучами являются прямые, параллельные волновому вектору. Этот вектор указывает направление распространения волны, а его модуль (волновое число), частота и скорость волны связаны соотно­шением (11.6). На рис. 11.3 изображены фазовые поверхности и лучи плоской волны.

11.4. Плоские электромагнитные волны *

Рассмотрим электромагнитное поле в пространстве, заполненном однородным диэлектриком, в котором отсутствуют свободные заряды и электрические токи, т.е. объемная плотность связанных зарядов и плотность тока равны нулю:

ρ=0, j=0

В таком случае уравнения Максвелла (10.1) - (10.4) принимают вид

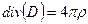
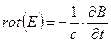
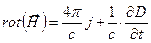
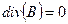(11.12)

где

D =εE, В =μH. (10.13)

rot E

div В =0,

Для однородной среды абсолютные диэлектрическая и магнитная про­ницаемости вещества постоянны: ε = const и μ = const. При помощи

соотношений (11.13) векторы D и В удобно исключить из системы урав­нений (11.12):

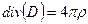→ divE=0

→

→

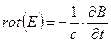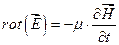
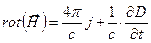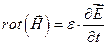
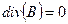→divH=0

Пусть векторы Е и Н зависят только от t и у:

Е = Е(t,у), H = H(t,y) (11.15)

Покажем, что эти функции могут быть решениями уравнений (11.14), а также, что среди решений уравнений (11.14) такого вида есть функции, описывающие плоские электромагнитные волны, распространяющиеся вдоль оси у.

Вычислим ротор и дивергенцию вектора E(t, у)

rot E = = +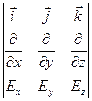

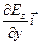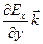
div =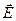

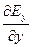
С учетом этих формул подстановка векторов (11.15) в равенства (11.14) приводит к системе уравнений

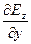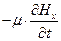= (11.16)

0= 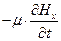(11.17)

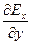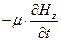- = (11.18)

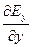=0 (11.19)

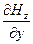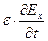= (11.20)

0= 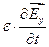(11.21)

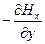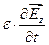= (11.22)

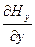=0 (11.23)

Из уравнений (11.19) и (11.21) следует, что Е_y = const. Очевидно, что постоянное электрическое поле в электромагнитной волне отсутствует. Поэтому положим

Е_у = 0 (11.24)

Аналогично, уравнения (11.17) и (11.23) приводят к равенству

Н_у=0. (11.25)

Оставшиеся неиспользованными уравнения можно разделить на две независимые системы. Первая состоит из уравнений (11.16) и (11.22) для функций E_z и Н_х, а вторая - из уравнений (11.18) и (11.20) для функций Е_х и Н_г. Выпишем уравнения первой системы:

=

=

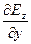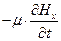
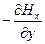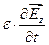
Исключим Н_х из этой системы. Для этого продифференцируем уравне­ние (11.16) по у, а уравнение (11.22) - по i. После несложных преобразо­ваний придем к уравнению

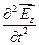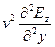= ; (16.26)

где

v= 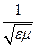(11.27)

Уравнение (11.26) есть волновое уравнение. Одно из его решений, опи­сывающих гармоническую волну, имеет вид

E_z(t,y) = E_m cos(ωt-ky+а) (11.28)

где E_m - амплитуда волны. Эта волна распространяется вдоль оси у в сторону возрастания у.

Функция

E_z(t,y) = E_m cos(ωt + ку + а)

также является решением волнового уравнения (11.26). Эта функция есть плоская гармоническая волна, распространяющаяся вдоль оси у в сторону убывания у.

Найдем функцию H_x(t,y), соответствующую функции (11.28). Для этого подставим выражение (11.28) в уравнения (11.16) и (11.22). Полу­чим:

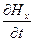= -( кЕ_m/μ)sin(ωt- к у + а),

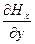= ωεE_m sin(ωt- ky +a)

Отсюда с учетом соотношений (11.6) и (11.27) найдем, что

Н_х = H_m cos(ωt- ky +a) (11.29)

Н_т = 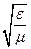Е_т (11.30)

В частном случае система уравнений (11.18) и (11.20) имеют нулевое

решение:

E_x = 0, Н_z = 0. (11.31)

Нетрудно проверить, что функции

E_x(t,y) = Е_т cos(ωt-ky+a),

H_z(t,y) = H_mcos(ωt- к у + а)

при условии (11.30) также являются решениями системы уравнений (11.18) и (11.20).

Итак, найдены решения уравнений Максвелла в виде плоских гармо­нических волн, распространяющихся вдоль оси у. Решениями уравнений Максвелла могут быть не только плоские гармонические волны. Вдоль оси у могут распространяться электромагнитные волны более сложной формы. Например, это может быть произвольная суперпозиция плос­ких гармонических волн. Для всех этих волн справедливы равенства (11.24) и (11.25). Вообще все электромагнитные волны обладают таким свойством. Проекции векторов Е и H на направление, вдоль которо­го распространяется электромагнитная волна всегда равны нулю. Это свойство называют поперечностъю электромагнитных волн.