Энергия электромагнитных волн.

Объемная плотность энергии электромагнитного поля W равна сумме объемных плотностей энергии электрического (w_e) и магнитного (w_m) полей.

Для поля в линейной изотропной среде, не обладающей сегнетоэлектрическими и ферромагнитными свойствами, w_e можно найти по формуле

w_e=dW_e/dV=½εε₀E²=½ED,

а w_m – по формуле

,

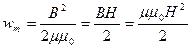поэтому

,

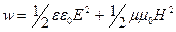Где ε и μ – относительные диэлектрические и магнитная проницаемость среды. Из соотношения

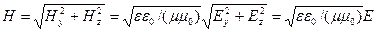
между модулями векторов E и H поля электромагнитной волны следует, что объемная плотность энергии электромагнитной волны

,

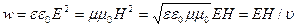Где ν – скорость электромагнитной волны в среде

.

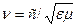В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления оси OX, напряженность поля .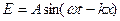

Соответственно объемная плотность энергии этой волны

.

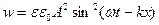Значение w в каждой точке поля периодически колеблется с частотой 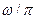в пределах от 0 до

.

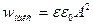Среднее за период значение w пропорционально квадрату амплитуды напряженности поля:

.

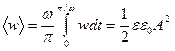Если плоская монохроматическая волна имеет произвольную (эллиптическую) поляризацию, то

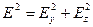
и отсюда получим

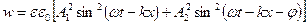
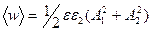
Вектор П плотности потока энергии электромагнитной волны называется вектором Умова-Пойтинга (вектором Пойтинга).

В случае переноса энергии бегущей монохроматической волной равна фазовой скорости этой волны. Вектор Умова-Пойтинга равен

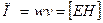
В случае плоской бегущей монохроматической волны, которая эллиптически поляризована, модуль вектора П равен

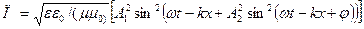
Если, в частности, волна линейно поляризована, то

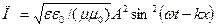
Интенсивность света.

Интенсивность

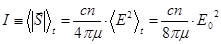— плотность потока энергии (энергия в единицу времени через единицу площади).

Связь интенсивности света с объемной плотностью энергии световой волны.

,

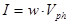где 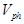— фазовая скорость света, хотя казалось бы, должна быть групповая.