Волновое уравнение. Из курса электричества мы уже знаем, что переменное магнитное поле создает вихревое электрическое поле

Из курса электричества мы уже знаем, что переменное магнитное поле создает вихревое электрическое поле. Линии этого поля замкнуты, оно существует независимо от электрических зарядов и только до тех пор, пока происходит изменение магнитного поля. На электрические заряды оно действует так же, как электростатическое поле, что следует из явления электромагнитной индукции.

Изучая взаимосвязь между электрическим и магнитным полями, Д. Максвелл создал теорию электромагнитного поля на основе двух постулатов (утверждений):

1) переменное магнитное поле создает в окружающем его пространстве вихревое электрическое поле;

2) переменное электрическое поле создает в окружающем его пространстве вихревое магнитное поле.

Когда конденсатор включен в цепь переменного тока, то между его обкладками имеется переменное электрическое поле, а это означает, что в том же пространстве должно быть магнитное поле. Таким образом, изменяющееся электрическое поле по его магнитному действию можно рассматривать как своеобразный электрический ток без зарядов. В отличие от тока проводимости Максвелл стал называть его током смещения. Итак, применяя термин «электрический ток» в широком смысле слова, т. е. включая в него и ток проводимости и ток смещения, можно утверждать, что магнитное поле создается только электрическим током и действует только на движущиеся заряды; электрическое же поле создается электрическими зарядами и переменным магнитным полем и действует на любые электрические заряды.

Описанное выше изменение электрического поля в конденсаторе создает в близлежащих точках окружающего пространства изменяющееся магнитное поле, которое в свою очередь создает в соседних точках электрическое поле, и т. д. Таким образом, во всем пространстве, где происходят изменения полей, одновременно существуют вихревые электрическое и магнитное поля, взаимно порождающие и поддерживающие друг друга. Поскольку эти поля неразрывно связаны, их общее поле условились называть электромагнитным полем.

Из сказанного выше следует, что если в какой-либо малой области пространства периодически изменять электрическое и магнитное поля, то эти изменения должны периодически повторяться и во всех других точках пространства, причем в каждой последующей точке несколько позже, чем в предыдущей. Иными словами, если создать электромагнитные колебания в какой-либо небольшой области, то от нее должны распространяться во все стороны электромагнитные волны с определенной скоростью[3]. Итак, из постулатов Максвелла следует, что в природе должны существовать электромагнитные волны.

Посмотрим теперь, как из уравнений Максвелла получается волновое уравнение вида (*.*), рассмотренное нами в главе 1. Зачем это надо? Ну прежде всего математически подтвердить наши качественные рассуждения. Но не только. Как мы помним коэффициент в правой части волнового уравнения есть квадрат скорости распространения волны. Таким образом, мы можем надеяться получить теоретическое предсказание для скорости электромагнитных волн, затем сравнить ее с измеренной экспериментально и, следовательно, подтвердить или опровергнуть нашу теорию. Проделаем это.

Нас интересует распространение электромагнитных волн в самом простом случае, например в воздухе. С хорошей точностью можно считать, что воздух является диэлектриком, притом однородным. Для такой среды уравнения Максвелла имеют вид:

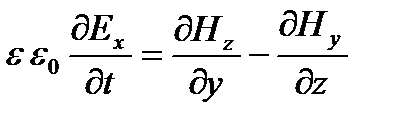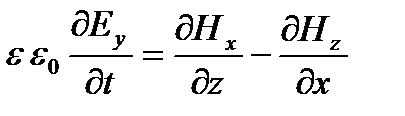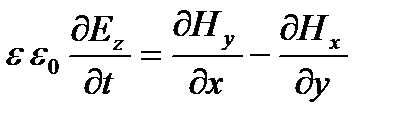; ; (1.1)

Здесь вектора Е и Н это напряженности электрической и магнитной составляющей электромагнитного поля, индексом снизу мы обозначаем соответствующую проекцию, ε₀ – электрическая постоянная, ε – относительная диэлектрическая проницаемость среды (в нашем случае – воздуха).

Уравнения (1.1) представляют собой систему дифференциальных уравнений в частных производных и математически выражают уже упомянутый нами факт: переменное электрическое поле создает в окружающем его пространстве вихревое магнитное поле..

Вторая группа уравнений Максвелла математически выражает другой упомянутый факт: переменное магнитное поле создает в окружающем его пространстве вихревое электрическое поле

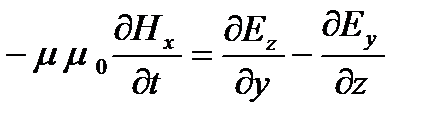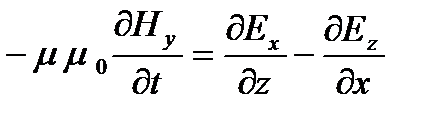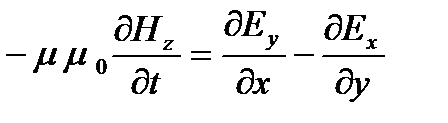; ; (1.2)

здесь μ₀ – магнитная постоянная, μ – магнитная проницаемость среды.

К этим уравнениям добавим еще два:

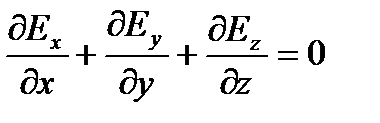(1.3)

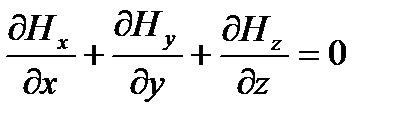(1.4)

Уравнения (1.1)-(1.4) представляют собой полную систему уравнений Максвелла в дифференциальной форме, в которых все входящие величины относятся к одной и той же точке поля и одному и тому же моменту времени.

Как Е, так и Н являются в общем случае функциями времени и координат x, y, z, т.е. всего 4-х переменных. Аналитически (как это не прискорбно) эти уравнения решаются только в очень ограниченном числе простейших случаев, поэтому их решают численно.

Далее мы ограничимся особенно простым случаем электромагнитного поля, когда Е и Н зависят от одной координаты х и от времени (одномерная задача). Это значит, что все пространство можно разбить на бесконечно тонкие плоские слои, внутри которых Е и Н имеют одно и то же значение во всех точках (рис. 1.1).

Как и у механических волн, у электромагнитных волн, поверхность, во всех точках которой колебания имеют одинаковую фазу, называют фронтом волны. В зависимости от того, какую форму имеет волновой фронт, мы говорим о плоских волнах (волновой фронт плоский), сферических, цилиндрических и т. д. Рассматриваемая одномерная задача соответствует, очевидно, плоским электромагнитным волнам.

Для одномерного случая уравнения Максвелла сильно упрощаются. Так как все производные по у и z равны нулю, то прежде всего из первого уравнения (1.1) следует, что 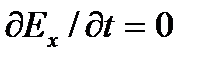, а из первого уравнения (1.2) — что 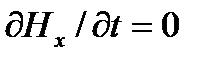. Это значит, что составляющие полей Е_х и Н_х не зависят от времени. Далее из (1.3) и (1.4) получается, что 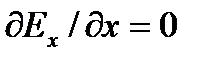и 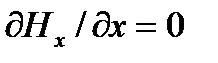, а значит, Е_х и Н_х не зависят также и от координаты. Поэтому

Е_х=const и Н_х=const

Остающиеся уравнения (1.1) теперь принимают вид

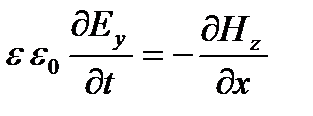
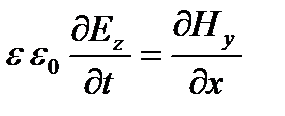
а уравнения (1.2) — вид

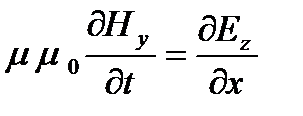
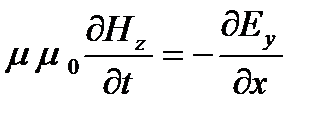
Эти четыре уравнения можно сгруппировать в две независимые группы, одна из которых связывает y-составляющие электрического поля и z-составляющие магнитного поля

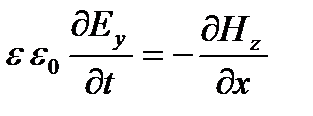
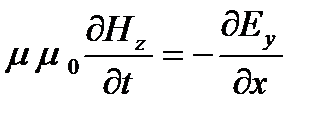
а другая — z-составляющие электрического поля и y-составляющие магнитного поля

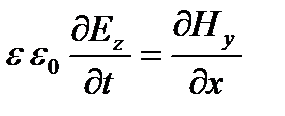
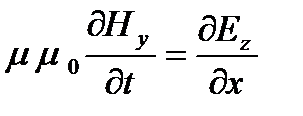
Отсюда следует, что меняющееся во времени электрическое поле Е_y вызывает появление только магнитного поля H_z, направленного вдоль оси Z, а переменное во времени магнитное поле H_z влечет появление электрического поля Е_y, целиком направленного вдоль оси Y. Или, иначе: в электромагнитном поле электрическое и магнитное поля перпендикулярны друг к другу. Такой же вывод вытекает и из второй пары уравнений.

Найденный результат позволяет положить без нарушения общности, что все электрическое поле направлено вдоль одной из осей, например вдоль оси У, а магнитное поле — вдоль оси Z (рис. 1.2). Поэтому в последних уравнениях можно положить, Е_y=E, Е_z = 0, H_z =H, H_y = 0, и мы находим окончательно уравнения Максвелла для одномерного случая в следующем простом виде:

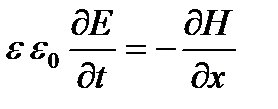
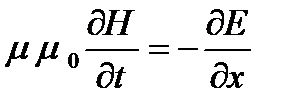(1.5)

Исключим из уравнений Максвелла (1.5) магнитное поле Н. Для этого умножим первое из уравнений на μ₀ μ и продифференцируем обе его части один раз по t:

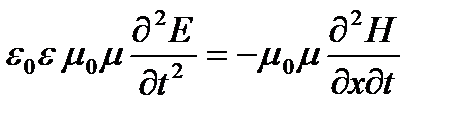
Второе уравнение продифференцируем по х:

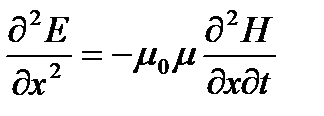
Так как правые части этих уравнений одинаковы, то, следовательно, равны и левые части, т. е.

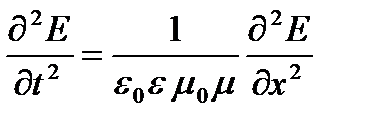(1.6)

Такое же уравнение мы получили бы и для Н, если бы из (1.5) исключили электрическое поле Е.

Уравнение (1.6) есть волновое уравнение, рассмотренное в главе 1. Отсюда следует, что поля Е и Н могут распространяться в пространстве, т. е. могут существовать электромагнитные волны.

Теперь ясно, что обещанное теоретическое значение скорости электромагнитных волн равно:

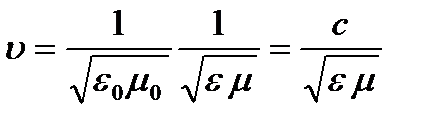(1.7)

где с есть скорость распространения при ε = μ = 1, т. е. в вакууме. Мы получили, таким образом, выражение для скорости распространения электромагнитных волн, которое соответствует опыту с=3·10⁸ м/c.

Уравнению (1.6) удовлетворяет, в частности, простейшая – синусоидальная волна:

,

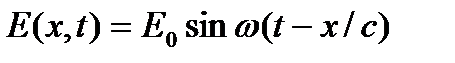в которой вектор Е распространяется вдоль оси ОХ со скоростью с; 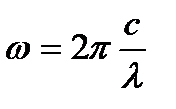– круговая частота; λ - длина волны.