Поток энергии в волновых процессах

Процесс распространения волны в каком-нибудь направлении в среде сопровождается переносом энергии колебаний в этом направлении. Допустим, что S есть часть фронта плоской волны в некоторый момент t (рис. 5.1). По истечении времени Δt фронт волны переместится на расстояние Δl=сΔt, вследствие чего частицы среды в объеме SΔl приводятся в колебательное движение. Обозначим через W энергию колебания частиц среды, содержащихся в единице объема; допустим, что объем сΔt очень мал и поэтому в пределах этого объема энергия W везде одинакова. Можно утверждать, что за время Δt среда в объеме SΔl через площадку S получила энергию WSΔl. Таким образом, за единицу времени через площадку S прошла энергия

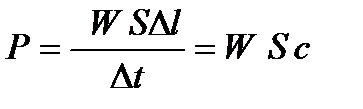
Величина Р есть поток энергии волны (в единицу времени) через площадку S (S ориентируют перпендикулярно к направлению распространения волны). Плотностью потока энергии называют энергию, проходящую в единицу времени через единицу площадки, перпендикулярной к направлению распространения волны:

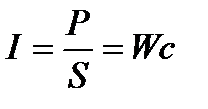(5.1)

Так как скорость распространения волны с есть вектор, то и плотность потока энергии есть векторная величина (он называется вектор Умова). Поток энергии измеряется в ваттах, плотность потока — в Вт/м².

В сферической волне, вызванной точечным источником колебаний, плотность потока энергии убывает обратно пропорционально квадрату расстояния от источника колебаний. Для доказательства допустим, что источник колебаний ежесекундно отдает в окружающую среду одну и ту же энергию, равную Е. Эта энергия равномерно распределяется по шаровой поверхности фронта волны S=4πR ², поэтому через единицу площади этой поверхности в единицу времени приходит энергия I= E/4πR² т.е. I~1/R². Это соотношение, так же как и формула (5.1), применимо, если только в среде не происходит превращения энергии колебательного движения в другие виды энергии, например в теплоту.

Найдем формулу для расчета W. Рассмотрим некоторый объем среды, размеры которого настолько малы по сравнению с длиной волны λ, что в пределах этого объема фазы и амплитуды колебаний для всех частиц можно считать одинаковыми. Обозначим массу одной частицы через m, число частиц в единице объема — п. Тогда полная энергия колебаний (сумма кинетической и потенциальной энергии) частиц, содержащихся в единице объема, будет равна:

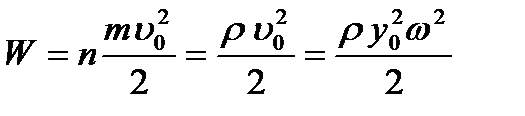
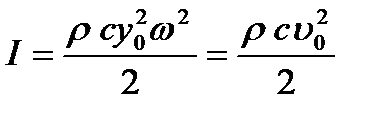
где ρ=nm — плотность среды; y₀ — амплитуда смещения; υ₀ = y₀ω — амплитуда скорости; ω — угловая частота колебаний частиц среды, 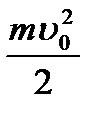- полная энергия гармонического осциллятора. Для сферической волны плотность потока энергии убывает обратно пропорционально квадрату расстояния от центра колебаний, поэтому амплитуда колебаний у₀ убывает обратно пропорционально первой степени этого расстояния.

Заметим, что, согласно формул (4.5), (4.6) и (3.4), максимумы избыточных давлений и плотностей в волне совпадают не с максимумами смещений у, а с максимумами скоростей частиц среды υ = dy/dt. Поэтому потенциальная энергия сжатых и растянутых участков среды изменяется в фазе с кинетической энергией колеблющихся частиц среды, т. е. вдоль волны оба эти вида энергии (потенциальная и кинетическая) одновременно приобретают наибольшие и наименьшие значения.

При распространении волны в среде происходит поглощение энергии, т. е. превращение механической энергии колебаний в беспорядочное (тепловое) движение частиц среды. Полагая, что в слое толщиной dх количество поглощенной энергии dI на единице площади пропорционально величине I и толщине слоя, получим

dI=-βIdx; .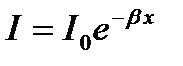

Величина β называется коэффициентом поглощения энергии волны в данной среде. Так как энергия волны пропорциональна квадрату амплитуды (смещения, скорости, избыточного давления или плотности), то при прохождении слоя среды толщиной х эти амплитуды будут убывать по закону

y_0x=y₀e^-αx; Δp=Δp₀e^-αx.

Величина α (равная β/2) называется коэффициентом затухания колебаний в среде. Для воздуха и некоторых других газов он пропорционален квадрату частоты колебаний: 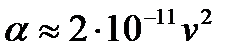c²/м; для воды (до ν=10⁶ Гц) 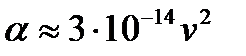c²/м т. е. в 700 раз меньше, чем в воздухе. Например, амплитуда ультразвуковых колебаний с частотой ν=10⁶ Гц уменьшается в e=2.71раза в воздухе на расстоянии 1/α = = 0.05 м, а воде—на расстоянии 33.4 м. Этим объясняется широкое применение звуковых и ультразвуковых волн при исследовании морей, при гидролокации и т. д.