Уравнение волны
При описании волнового процесса требуется найти амплитуды и фазы колебательного движения в различных точках среды и изменение этих величин с течением времени. Эта задача может быть решена, если известно, по какому закону колеблется и как взаимодействует со средой тело, вызвавшее волновой процесс. Однако во многих случаях не существенно, каким телом возбуждена данная волна; решается более простая задача: дано состояние колебательного движения в некоторых точках среды в определенный момент времени, например известно расположение фронта волны или волновой поверхности; требуется определить состояние колебательного движения в других точках среды эта задача выходит за пределы нашего курса. Здесь же мы найдем связи между состояниями колебательного движения в различных точках среды в простейшем случае, когда в этой среде распространяется плоская или сферическая синусоидальная волна.
Допустим, что волновой процесс распространяется в положительном направлении оси ОХ, т. е. в сторону возрастания координаты х. Обозначим через у колеблющуюся величину; этой величиной могут быть: смещение частиц среды относительно их положения равновесия, отклонение давления или плотности в данном месте среды от равновесного значения и т. д. Для простоты рассуждений предположим, что распространяющаяся волна — синусоидальная, т. е. в каждой точке среды величина у изменяется со временем по гармоническому закону. Мы разумеется помним, что означают слова «по гармоническому закону». Ну а кто не помнит, напомним. Это означает, что зависимость от времени колеблющейся величины выражается формулой:
y(t)=y0 sin(ωt + φ) (3.1)
здесь выражение ωt + φ называется фазой гармонического колебания, φ – начальная фаза, y0 - амплитуда колебаний.
Сделаем еще одно определение. Колебание (3.1) происходит с одной единственной частотой ω . Такое колебание называется умным словом монохроматическим. Это определение пришло к нам из оптики и в буквальном переводе (с не помню с какого языка) означает одноцветное. Дело в том, что свет различной частоты имеет разный цвет (красный, желтый и т.п.), поэтому свет какого-то определенного цвета имеет определенную частоту. Ну вот так и назвали. Этим определением пользуются и в других разделах физики, в частности и в теории волн в упругой среде. Но вернемся к нашим волнам.
Допустим, что начало отсчета времени выбрано так, что в точке О при t = 0, у = 0, т. φ =0 тогда
y(t)=y0 sin ωt
где ω = 2π/Т — угловая частота; Т — период; ωt — аргумент синуса (определяющий значение колеблющейся величины в каждый заданный момент времени) есть фаза колебаний в точке О. Требуется найти фазу колебаний в любой другой точке А, отстоящей от О на расстоянии х. Если мы будем знать фазу колебаний в любой точке (ясно, что теперь она будет зависеть от х), то мы будем знать и аргумент синуса, а значит и значение колеблющейся величины в любой момент времени в любой точке.
Так как точка А расположена относительно О в направлении распространения волны, то в данный момент времени t в этой точке будет такое состояние колебательного движения, какое было в точке О на x/с секунд раньше[1]; здесь с -есть скорость распространения фазы колебаний в направлении ОХ. Таким образом, фаза колебаний в точке А в момент t равна фазе колебаний в точке О в более ранний момент t-x/с, т. е. равна ω (t-x/с).
Следовательно, значение колеблющейся величины в точке А в момент времени t:
y(x,t)=y0 sin ω(t-x/с) (3.2)
Это соотношение называется уравнением синусоидальной волны, а с — ее фазовой скоростью.
Допустим теперь, что волна распространяется в обратном направлении, т.е. от А к О, в сторону убывания координаты х. Тогда определенное состояние колебания, т. е. определенная фаза волны, достигает точки А на τ=x/с секунд раньше, чем точки О, следовательно, фаза в точке А в данный момент времени больше фазы в точке О на ωτ=ωx/с. Если по-прежнему принять фазу в точке О в момент t равной ωt, то в точке А в этот же момент времени фаза будет равна ωτ=ω(t+x/с). Таким образом, уравнение синусоидальной волны можно написать в общем виде:
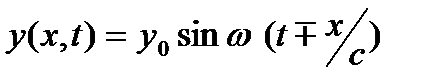 (3.3)
(3.3)
где знак «минус» берется для волны, распространяющейся в направлении возрастания х, а плюс — в обратном направлении.
При выводе формулы (3.3) предполагалось, что амплитуда колебаний y0 по мере распространения волны не изменяется, и среда однородная (т. е. скорость распространения фазы колебаний везде одинаковая). Эти два предположения означают, что мы рассматривали плоскую волну, у сферической волны, как мы увидим в дальнейшем, амплитуда колебаний уменьшается обратно пропорционально расстоянию.
Мы уже знаем, что расстояние λ, пройденное волной (т. е. определенной фазой колебаний) за один период колебаний, называется длиной волны, очевидно,
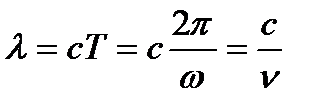 ;
; 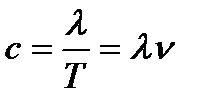
В уравнении волны (3.2) колеблющаяся величина зависит от двух переменных: х и t. Если найти производную от y(x,t) по времени, полагая х постоянной, то эта частная производная
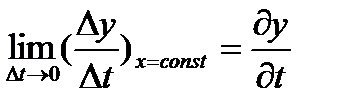
показывает скорость изменения колеблющейся величины в данной точке среды. Производная же от у по х при постоянном t
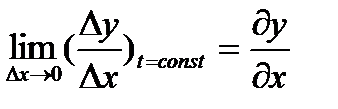
есть разность значений колеблющейся величины, рассчитанная на единицу расстояния между точками среды (Δx =x2-x1), т. е. показывает, как резко увеличивается или уменьшается у вдоль оси ОХ (в данный момент времени t) колеблющаяся величина.
Найдем частные производные от колеблющейся величины у по времени при постоянном х:
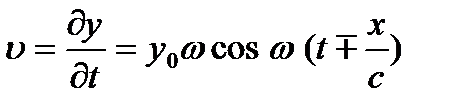
(3.4)
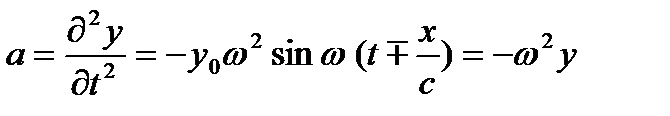
Если y есть смещение частиц среды при колебаниях, то υ и а будут скоростью и ускорением этих частиц при их колебательном движении в точке с координатой х. Амплитудные значения этих величин связаны между собой:
υ0=y0 ω; a= y0 ω2 = υ0 ω .
Частные производные от у по х при постоянном t будут равны:
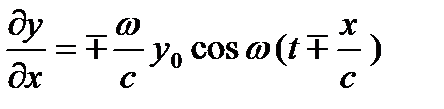 ,
,
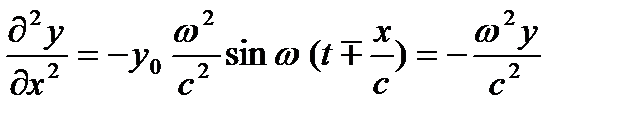 .
.
Следовательно,
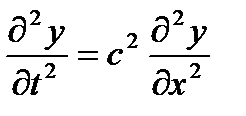 (3.5)
(3.5)
это и есть дифференциальное уравнение плоской бегущей волны, распространяющейся по оси ОХ. Оно получено нами из уравнения волны (3.3). Однако можно сделать и обратное заключение: если какая-нибудь физическая величина у = у (х, t) зависит от времени и координат так, что ее частные производные удовлетворяют уравнению (3.5), то величина у распространяется в среде в виде плоской волны [см. уравнение (3.3)] со скоростью
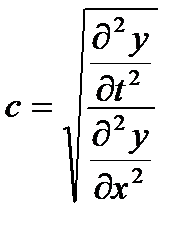
и частотой колебаний
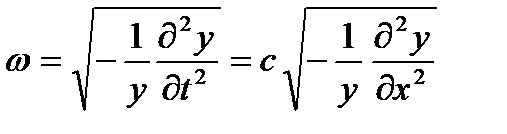
Звук
Напомним физическую природу звуковых явлений. Как известно, для получения чистого звука пользуются камертоном*. Когда камертон издает звук, то шарик отскакивает от его ножки, так как она колеблется (рис. 4.1). Опыт показывает, что источником звука всегда является какое-либо колеблющееся тело, которое в процессе своих колебаний создает в окружающей среде механические волны (рис. 4.2). Когда эти волны достигают уха человека, то они приводят в вынужденные колебания барабанную перепонку внутри уха, и человек ощущает звук. Механические волны, которые вызывают у человека ощущение звука, называют звуковыми.
Звуковые волны в воздухе состоят из сгущений и разрежений, т. е. являются продольными. Ясно, что ощущение звука человек может получить только в том случае, когда между источником звука и ухом человека имеется среда, в которой могут распространяться звуковые волны..

Изучение звуковых явлений показало, что далеко не всякие механические волны могут вызвать ощущение звука у человека. Оказывается, что только волны, частота колебаний которых находится в пределах от 16 до 20 000 Гц, являются звуковыми. Это знает всякий, кто интересуется музыкой вообще и воспроизведением музыки в частности. Главный параметр любого уважающего себя музыкального центра - полоса пропускания. Чем она ближе к упомянутой, тем центр лучше, или дороже[2]. Заметим, что верхняя и нижняя границы частот этих колебаний у отдельных людей могут немного отличаться от указанных выше.
Итак, человек ощущает звук, если выполняются следующие четыре условия:
1) имеется источник звука;
2) имеется упругая среда между ухом и источником звука;
3) частота колебаний источника звука находится между 16 и 20000 Гц;
4) мощность звуковых волн достаточна для получения ощущения звука у человека.
 Итак, при распространении в среде упругих (в частности, звуковых) колебаний частицы среды совершают колебательное движение относительно своих положений равновесия. Можно было бы описывать волновое движение, учитывая только смещения и скорости частиц среды. Однако при наличии беспорядочного теплового движения частиц пользоваться таким описанием неудобно. Поэтому принято упругую (и частности звуковую) волну характеризовать периодическими изменениями давления и плотности, которые происходят при последовательных сжатиях и растяжениях (расширениях, разряжениях) среды. Обозначим, например, давление и плотность воздуха в равновесном состоянии через р0 и ρ0 а их мгновенные значения в данном месте через р и ρ. Тогда ,для описания звуковой волны в воздухе можно интересоваться периодическими изменениями избыточного давления Δр=р-р0 или избыточной плотности Δρ =ρ –ρ0 .
Итак, при распространении в среде упругих (в частности, звуковых) колебаний частицы среды совершают колебательное движение относительно своих положений равновесия. Можно было бы описывать волновое движение, учитывая только смещения и скорости частиц среды. Однако при наличии беспорядочного теплового движения частиц пользоваться таким описанием неудобно. Поэтому принято упругую (и частности звуковую) волну характеризовать периодическими изменениями давления и плотности, которые происходят при последовательных сжатиях и растяжениях (расширениях, разряжениях) среды. Обозначим, например, давление и плотность воздуха в равновесном состоянии через р0 и ρ0 а их мгновенные значения в данном месте через р и ρ. Тогда ,для описания звуковой волны в воздухе можно интересоваться периодическими изменениями избыточного давления Δр=р-р0 или избыточной плотности Δρ =ρ –ρ0 .
Выясним, при каких условиях в упругих средах возможны гармонические волны вида (3.3). Выделим перпендикулярно к ОХ некоторую площадку S (рис. 4.3) и слой малой толщины Δl. Допустим, что в положении I избыточное давление слева равно Δр1, а справа 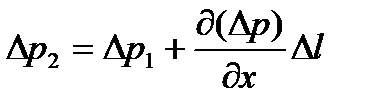 , следовательно, на выделенный элемент среды будет действовать результирующая сила Δ F=S ( Δ р1 – Δ р2 ) =
, следовательно, на выделенный элемент среды будет действовать результирующая сила Δ F=S ( Δ р1 – Δ р2 ) = 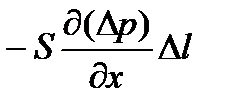 . Масса этого элемента Δm = ρ S Δl, где ρ — средняя плотность среды в объеме элемента. Тогда, согласно второму закону Ньютона рассматриваемый элемент среды будет иметь ускорение
. Масса этого элемента Δm = ρ S Δl, где ρ — средняя плотность среды в объеме элемента. Тогда, согласно второму закону Ньютона рассматриваемый элемент среды будет иметь ускорение
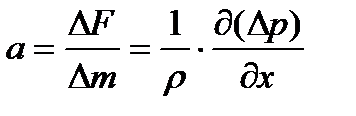
(знак «минус» означает, что если избыточное давление Δр в положительном направлении х возрастает, то сила ΔF и ускорение а будут направлены в обратную сторону).
Так как смещение частиц, среды у зависит от двух переменных: времени и координаты, то ускорение элемента запишем в виде 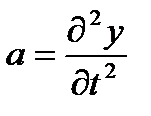 ; тогда
; тогда
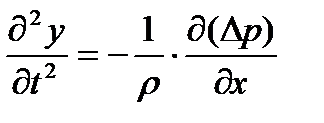 (4.1)
(4.1)
 Исследуем правую часть этой формулы. Если бы все частицы среды, находящиеся в рассматриваемом элементе, имели бы одинаковое смещение у, то объем элемента, следовательно, и давление р и плотность ρ внутри него оставались бы постоянными. В этом случае правая часть уравнения (4.1) будет равна нулю и упругой волны в среде не обнаружится. Поэтому необходимо допустить, что при переходе из положения I в II одна грань рассматриваемого элемента среды смещается на у, а другая - на у + Δу. При таком перемещении объем элемента изменится, вследствие чего давление р станет функцией от координаты х и правая часть уравнения (4.1) будет отлична от нуля. Однако в формуле (4.1) имеются две переменные величины у и р; если исключить одну из них, например давление р, то получим дифференциальное уравнение для смещения элементов среды от положения равновесия. Для этой цели сначала учтем, что величину Δу следует полагать пропорциональной толщине элемента среды Δl:
Исследуем правую часть этой формулы. Если бы все частицы среды, находящиеся в рассматриваемом элементе, имели бы одинаковое смещение у, то объем элемента, следовательно, и давление р и плотность ρ внутри него оставались бы постоянными. В этом случае правая часть уравнения (4.1) будет равна нулю и упругой волны в среде не обнаружится. Поэтому необходимо допустить, что при переходе из положения I в II одна грань рассматриваемого элемента среды смещается на у, а другая - на у + Δу. При таком перемещении объем элемента изменится, вследствие чего давление р станет функцией от координаты х и правая часть уравнения (4.1) будет отлична от нуля. Однако в формуле (4.1) имеются две переменные величины у и р; если исключить одну из них, например давление р, то получим дифференциальное уравнение для смещения элементов среды от положения равновесия. Для этой цели сначала учтем, что величину Δу следует полагать пропорциональной толщине элемента среды Δl:
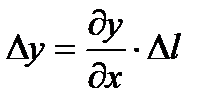 ,
,
где 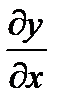 показывает, какое изменение смещения у приходится на единицу длины вдоль оси ОХ.
показывает, какое изменение смещения у приходится на единицу длины вдоль оси ОХ.
Тогда относительное изменение объема элемента будет равно:
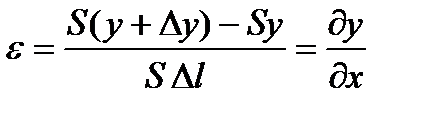 .
.
Масса среды в элементе объема не изменяется, поэтому относительное увеличение плотности будет равно относительному уменьшению объема элемента, т.е.
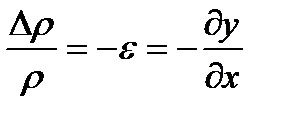 .
.
Теперь для того, чтобы рассчитать изменение избыточного давления Δр внутри элемента, необходимо знать зависимость Δр от ρ или ε.
Если среда – твердое тело, то при малых деформациях можно воспользоваться законом Гука: р= εЕ. Относительное удлинение или сжатие элемента объема будет (для плоской волны S = const) совпадать с относительным изменением его объема; напряжение сжатия или растяжения можно полагать равным среднему значению Δр внутри элемента, причем увеличение Δр сопровождается уменьшением объема элемента, поэтому
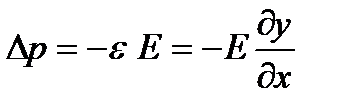 ;
; 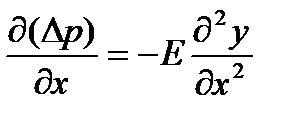 .
.
Подставив в формулу (4.1), получим дифференциальное уравнение плоской волны, распространяющейся в твердых телах:
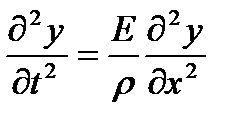 (4.2)
(4.2)
Сравнивая уравнения (4.2 ) и (3.4 ), замечаем, что величину Е/ρ следует отождествить с квадратом скорости распространения волны:
 (4.3)
(4.3)
Для железа, например, Е=2·1011 H/м2, ρ=7800 Кг/м3, и вычисляя получаем скорость звука V≈5100 м/c.
В газах процессы сжатия и расширения описываются уравнением
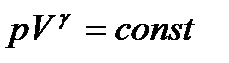
где р – давление, V - удельный объем , а γ – некоторая постоянная величина, зависящая от того как происходят процессы сжатия и расширения. Из этого уравнения следует:
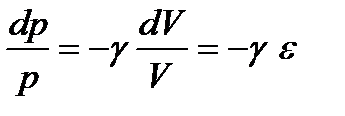 .
.
Если избыточное давление мало по сравнению с давлением газа р0 (а так при обычных условиях и бывает) то
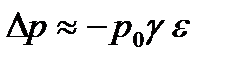 ;
; 
Подставив это выражение для 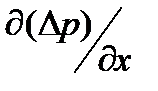 в формулу (4.1), вновь получим дифференциальное уравнение (3.4) плоской волны, причем скорость распространения оказывается равной (полагая
в формулу (4.1), вновь получим дифференциальное уравнение (3.4) плоской волны, причем скорость распространения оказывается равной (полагая 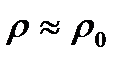 )
)
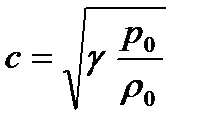 (4.4)
(4.4)
Дифференциальное уравнение плоской волны и формулы (4.3) и (4.4) для скоростей распространения получены при предположении, что избыточные давления Δр и плотности Δρ малы. Найдем изменение этих величин со временем; для любой среды, полагая 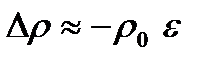 , получим для плотности:
, получим для плотности:
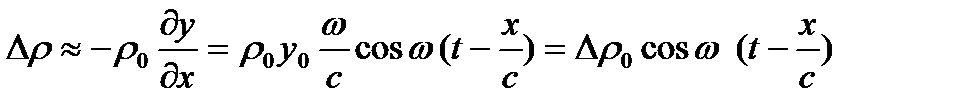 (4.5)
(4.5)
где через Δρ0 обозначена амплитуда колебаний плотности среды в волне:
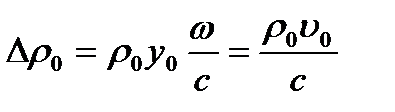
Для колебаний давления Δ р также получаются формулы, одинаковые для всех сред:
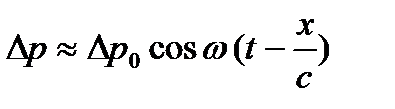 ; Δ р0=ρ0 υ0 с (4.6)
; Δ р0=ρ0 υ0 с (4.6)
Таким образом, Δ р и Δ ρ пропорциональны не смещению частиц среды у, а их скоростям υ.
Из уравнений (4.5) и (4.6) можно получить общее выражение для скорости распространения плоской волны в упругой среде
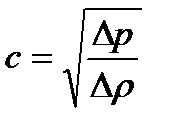 или
или 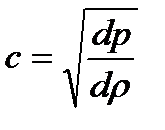
Дата добавления: 2015-06-12; просмотров: 1860;
