Стоячие волны

Особым примером результата интерференции двух волн служат так называемые стоячие волны, образующиеся в результате наложения двух встречных волн с одинаковыми амплитудами.

Предположим, что две гармонические волны с одинаковыми амплитудами, длиной волны 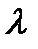, частотой 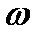и волновым числом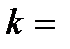 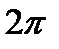/ 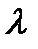, распространяются — одна по направлению положительной оси х, другая — по направлению отрицательной оси х. Если начало координат взять в такой точке, в которой встречные волны имеют одинаковые фазы, и выбрать отсчет времени так, чтобы начальные фазы оказа­лись равными нулю, то уравнения обеих волн можно напи­сать в следующем виде: для волны, идущей в сторону положитель­ной оси х,

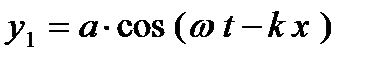
и для волны, идущей в сторону отрицательной оси х,

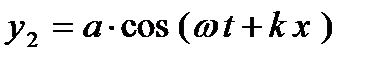
Сложение этих двух волн дает

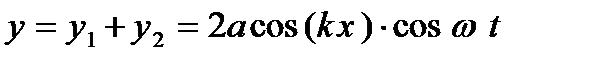
здесь мы раскрыли значение косинусов от сложных аргументов и произ­вели сокращения. Множитель cos 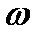t показывает, что в точках среды возникает колебание с той же частотой 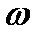. что и колебания встречных волн.

Множитель 2 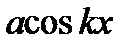, не зависящий от времени, выражает амплитуду А результирующего колебания; точнее — амплитуда, как величина существенно положительная, равна абсолютному значению этого множителя:

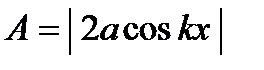(7.1)

Таким образом, амплитуда колебания зависит от координаты х. Возникшее колебание носит название стоячей волны. В определенных точках амплитуда стоячей волны равна сумме амплитуд обоих слагаемых колебаний, такие точки называются пучностями, в других точках результирующая амплитуда равна нулю, эти точки называются узлами стоячей волны.

Определим координаты точек пучностей и узлов. Амплитуда, определяемая равенством (7.1), максимальна в точках, для которых

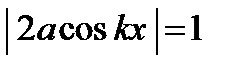
Отсюда положение пучностей определится условием, 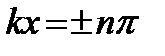где n =0, 1, 2,... Следовательно, координаты пучностей равны

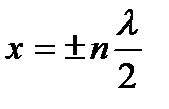(7.2)

где n = 0, 1, 2,...

Расстояние между соседними пучностями мы получим, если возьмем разность двух значений x, определяемых формулой (7.2) для двух последовательных значений n, откуда 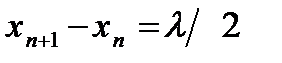,т.е. расстояние между двумя соседними пучностями равно половине длины тех волн, в результате интерференции которых образуется данная стоячая волна. Очевидно, в местах пучностей колебания обеих волн все время совершаются в одной фазе.

В узлах амплитуда результирующего колебания равна нулю, откуда по формуле (7.1) условие образования узлов:

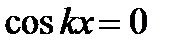или ,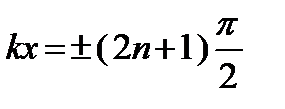

следовательно, координаты узлов равны 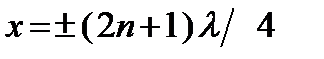,а значит, расстояние узла от ближайшей пучности равно 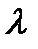/4, т.е. узлы и пучности отстоят друг от друга на четверть длины волны. Узлы образуются в тех местах, где колебания в обеих волнах всё время совершаются в противоположных фазах.

Так как в данный момент времени множитель cos 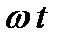имеет для всех точек одинаковое значение, то все точки между двумя узлами колеблются в одинаковых фазах, т. е. они одновременно достигают максимальных отклонений, одновременно проходят через положения равновесия и т. д. Точки, лежащие по обе стороны одного и того же узла, колеблются в противоположных фазах, т. е. достигают одновременно крайних, но противоположных по знаку смещений, проходят одновременно положение равновесия, но с противоположно направленными скоростями и т. д. Схема колебаний точек в стоячей волне указана на рис.7.1 а и б, где нанесены положения колеблющихся точек для двух моментов времени, отстоящих на полпериода.

Образование стоячих волн происходит обычно при интерференции бегущей вперед и отраженной волн. Например, если один конец струны укрепить неподвижно, то отраженная в месте закрепления струны волна будет интерферировать с бегущей вперед и образовывать стоячую волну. Узловые точки, остающиеся при этом неподвижными, находятся друг от друга на расстоянии, равном половине длины бегущей волны; в месте закрепления струны, т.е. на границе, где происходит отражение волны, получается узел. Точно так же происходит образование стоячих волн в трубе, заполненной воздухом и закрытой твердой стенкой с одной стороны. Здесь отраженние происходит от твердой стенки, и на границе так же образуется узел, так как слой воздуха непосредственно примыкающий к границе не участвует в волновом движении.

Вообще же говоря, на границе отражения может образоваться или узел, или пучность; это зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, более плотная, чем среда, в которой распространяется волна, то на границе получается узел. Если среда, от которой происходит отражение, менее плотная, чем та, в которой распространяется волна, то на границе получается пучность.

Образование узла на границе отражения от более плотной среды объясняется тем, что волна, отражаясь от более плотной среды, в месте отражения меняет свою фазу на прямо противоположную; тогда у границы складываются колебания противоположных направлений, что и ведет к образованию узла.

Так как фаза меняется на противоположную на расстоянии половины длины волны, то этот факт принято называть „потерей полволны".

Отражаясь от менее плотной среды, волна не меняет фазы в месте отражения, поэтому потери полволны не происходит. Благодаря этому фазы падающей и отраженной волн у границы одинаковы, и в этом месте получается пучность в результате сложения колебаний одинаковых фаз.