Энергия и импульс электромагнитного поля

Наверное вы уже поняли, что основные свойства волн не зависят от их природы. Это касается и такого важного свойства как перенос энергии. Подобно механическим волнам, электромагнитные переносят энергию.

Электромагнитная волна в направлении своего распространения переносит некоторое количество энергии. Она содержится в электрическом и магнитном полях и пропорциональна квадратам напряженностей Е и Н этих полей.

Действительно, через 1 м² площадки, ориентированной перпендикулярно к направлению распространения волны, за единицу времени пройдет вся та энергия, которая содержится в объеме параллелепипеда с основанием 1 м² и высотой, равной скорости распространения υ. Эта энергия является важной характеристикой электромагнитного излучения (плотностью потока энергии) и обозначается через I. Так как в единице объема электрического и магнитного полей содержится энергия

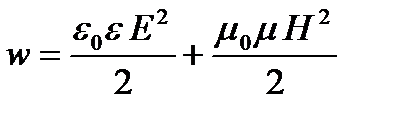(3.1)

то, имея в виду выражения (1.7), получим

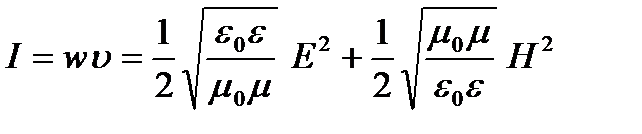
и учитывая (2.4):

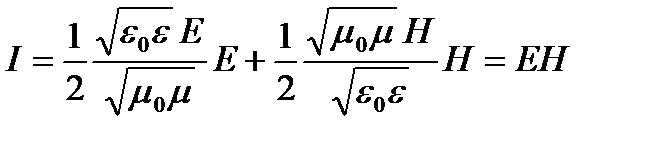(3.2)

И все бы хорошо, только мы не забыли, что и Е и Н величины векторные, да и сама плотность потока энергии тоже вроде как должна бы кроме величины характеризоваться еще и направлением. Т.е. из двух векторов Е и Н нужно соорудить третий вектор I, причем так, что бы выполнялось (3.2). Как из двух векторов сделать третий? Кроме как векторное произведение ничего в голову не приходит. Вот и английскому ученому Пойнтингу не пришло. Он и ввел вектор плотности потока электромагнитной энергии:

I=[EH] (3.3)

который так и стали называть – вектор Пойнтинга.

Для особо продвинутых отметим, что исходя из уравнений Максвелла, можно совершенно строго доказать следующую важную теорему о движении энергии в электромагнитном поле (теорема Пойнтинга). Выделим внутри произвольной среды некоторый объем τ, ограниченный поверхностью S (рис. 3.1). Обозначим далее полную энергию, заключенную внутри объема τ, через W. Тогда

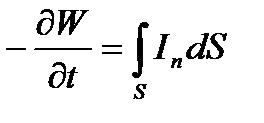
Здесь I_n — нормальная к поверхности составляющая вектора Пойнтинга, выражаемого формулой (3.3), а интегрирование производится по всей замкнутой поверхности S. При этом положительным считается направление внешней нормали п (рис. 3.3) т. е. поток 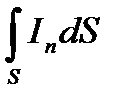считается положительным, если линии по-

тока энергии I выходят изнутри объема наружу.

Величина 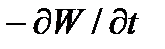есть уменьшение полной энергии внутри объема τ за единицу времени. Согласно закону сохранения энергии она должна равняться той энергии, которая выходит через поверхность S за единицу времени наружу. Отсюда следует, что энергия, выходящая через поверхность S за единицу времени, выражается потоком вектора I через замкнутую поверхность S, ограничивающую рассматриваемый объем. Величину же I_n можно истолковать как энергию, которая проходит через единицу поверхности в единицу времени.

Теорема Пойнтинга выражает интуитивно понятный факт: то, что делается на границе области, должно определяться тем, что происходит внутри нее1.

Давайте теперь, пользуясь формулой (3.2) (или (3.3), что одно и то же, но (3.2) выглядит проще) посчитаем энергию, которую переносит простейшая монохроматическая волна. Электрическая и магнитная составляющие такой волны будут:

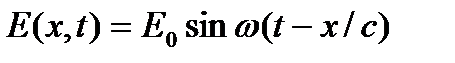
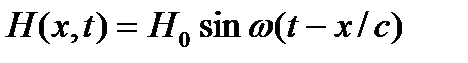(3.4)

Здесь мы, опять же для простоты, считаем, что дело происходит в вакууме, и что начальная фаза равна нулю. Тогда из (3.2):

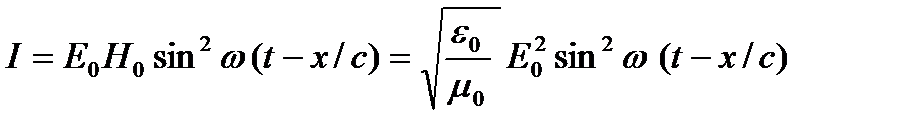(3.5)

это та энергия, которая переносится за единицу времени, через площадку единичной площади, перпендикулярную направлению распространения волны и расположенную в точке с координатой х. Как то не очень понятно получилось: I зависит от времени, от координаты, причем при фиксированном х зависит как sin², т.е. периодически, а значит, через период все в этой точке х повторяется. Это наводит на мысль об усреднении по времени в пределах периода. Функции вида (3.4) имеют период 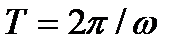, и усреднение I(x,t) в пределах периода выглядит так:

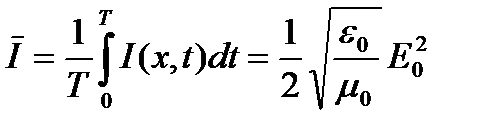
Это выглядит значительно проще. Средний за период поток энергии электромагнитной волны пропорционален квадрату амплитуды этой волны и называется интенсивностью, как и в случае упругих волн.