Волновой пакет

Понятие фазовой скорости, введенное нами ранее, применимо только к строго монохроматическим волнам, которые реально не осуществимы, так как они должны были бы существовать неограниченно долго во времени и быть бесконечно протяженными в пространстве.

В действительности мы всегда имеем более или менее сложный импульс, ограниченный во времени и в пространстве. При наблюдении такого импульса мы можем выделять какое-нибудь определенное его место, например, место максимальной напряженности того электрического или магнитного поля, которое представляет собой электромагнитный импульс. Скорость импульса можно отождествить со скоростью распространения какой-либо его точки, например, точки максимальной напряженности поля. При этом, однако, надо предполагать, что импульс наш сохраняет при распространении свою форму или, во всяком случае, деформируется достаточно медленно или периодически восстанавливается. Для выяснения этого обстоятельства мы можем представить импульс как наложение бесконечно большого числа близких по частоте монохроматических волн (представление импульса в виде интеграла Фурье). Если, например, все эти монохроматические волны разной длины распространяются с одной и той же фазовой скоростью, (среда не имеет дисперсии), то с той же скоростью перемещается и импульс как целое, сохраняя неизменной свою форму.

Однако среда (за исключением вакуума) обычно характеризуется дисперсией, т. е. монохроматические волны распространяются с различными фазовыми скоростями, зависящими от их длины, и импульс начинает деформироваться. В таком случае вопрос о скорости импульса становится более сложным. Если дисперсия не очень велика, то деформация импульса происходит медленно, и мы можем следить за перемещением определенной амплитуды ноля в волновом импульсе, например, максимальной амплитуды поля. Однако скорость перемещения импульса, названная Рэлёем групповой скоростью, будет отличаться от фазовой скорости любой из составляющих его монохроматических волн и должна быть предметом специального расчета.

Для простоты вычисления мы будем представлять себе импульс как совокупность двух близких по частоте синусоид одинаковой амплитуды, а не как совокупность бесконечного числа близких синусоид. При этом упрощении основные черты явления сохраняются. Наложение таких близких по частоте синусоид дает импульс, форма которого изображена на рис. 3.1 (биения близких по частоте колебаний). Итак, наш импульс, или, как принято говорить, группа волн1, составлен из двух волн

y₁=asin(ω₁ t - k₁x) и y₂=asin( ω₂ t – k₂x)

где амплитуды приняты равными, а частоты и длины волн мало отличаются друг от друга, т. е.

ω₁ =ω₀ +δω ω₂ =ω₀ – δω k₁ =k₀ + δk k₂ =k₀ – δk

где δω и δk — малые величины. Импульс (группа волн) у есть сумма y₁ и y₂, т. е.

y=y₁ + y₂= asin(ω₁ - k₁x)+ asin( ω₂t – k₂x)=2acos(t δω - xδk) sin(ω₀ t – k₀x)

Вводя обозначения A= 2acos(t δω - xδk) представим наш импульс в виде y=A sin(ω₀ t – k₀x), где А не постоянно, но меняется во времени и пространстве, однако меняется медленно, ибо δω и δk — малые (по сравнению с ω₀ и k₀) величины. Поэтому, допуская известную небрежность речи, мы можем считать наш импульс синусоидой с медленно изменяющейся амплитудой.

Выделив на импульсе какую-нибудь точку с определенным значением А, например точку, где А максимально, мы определим скорость перемещения этой точки, которая и характеризует скорость распространения импульса. Таким образом, скорость импульса (группы), которую, согласно Рэлею, называют групповой скоростью, есть скорость перемещения амплитуды, а, следовательно, и энергии, переносимой движущимся импульсом.

Для нахождения групповой скорости и надо написать условие постоянства амплитуды, т.е.

t δω – xδk=const

Дифференцируя, находим t δω - xδk = 0, или

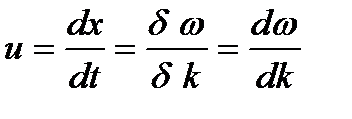
Итак, монохроматическая волна характеризуется фазовой скоростью υ=ω/k , означающей скорость перемещения фазы, а импульс характеризуется групповой скоростью u=dωd/k, соответствующей скорости распространения энергии поля этого импульса.

Нетрудно найти связь между u и υ. В самом деле,

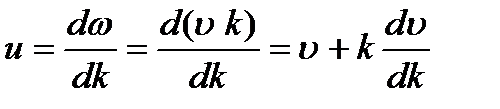
или, так как k=2π/λ и, следовательно, dk= - (2π / λ²) dλ ,

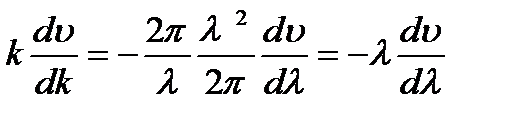
т. е. окончательно

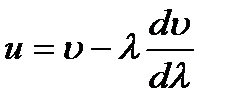- формула Рэлея