Увеличение

Выберем в качестве светящегося предмета линию А₁В₁, перпендикулярную к оси, и построим ее изображение А₂В₂ (рис. 6.1). Отношение линейных размеров изображения (y₂ = A₂B₂) и предмета (y₁ = A₁B₁) носит название линейного или поперечного увеличения :

V=y₂ / y₁=A₂B₂ / A₁B₁

Приписывая А₁В₁ и A₂B₂ знаки (как обычно в геометрии), получим, что увеличение положительно, если изображение прямое, и отрицательно, если изображение перевернутое. Из треугольников A₁B₁S и A₂B₂S имеем

y₁ / a₁ = tg i , y₂ / a₂ =tg r .

При малых размерах A₁B₁ и A₂B₂

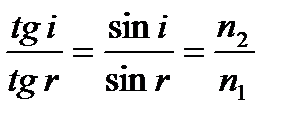
т.е.

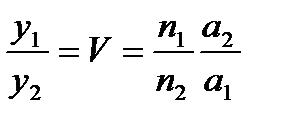
или (6.1)

Для преломляющей системы п₁ и п₂ всегда положительны, так что знак V определится знаком отношения а₂ /а₁. Для расположений, соответствующих действительному изображению (см. рис. 6.1), а₁ и а₂ имеют разные знаки, т. е. V отрицательно, и изображение перевернутое; для мнимых изображений — наоборот.

Для зеркал п₁/п₂ = —1, т. с. V = —а₂/а₁. В случае действительного изображения а₁, и а₂ имеют одинаковые знаки, т. е. V <0 и изображение перевернутое; в случае мнимого изображения знаки а₁ и а₂ различны, V > 0, изображение прямое. Для плоского зеркала (а₁ = — а₂) V = 1, т. е. изображение прямое и натуральной величины.

Сопряженные плоскости называются главными, если для них V = 1, т. е. изображение получается прямым и в натуральную величину объекта. Нетрудно видеть, что для сферической поверхности главные плоскости совпадают между собой и представлены плоскостью, касательной к сфере в точке S, т. е. а₁ = а₂ = 0. В соответствии с этим и фокусные расстояния сферической поверхности следует считать расстояниями от главных плоскостей до фокусов. На рис. 6.1 изображены также углы u₁ и u₂, определяющие максимальное раскрытие (апертуру) пучков, падающих на поверхность Σ (угол 2и₁), и сопряженных им изображающих пучков (угол 2u₂). Предельное значение этих углов определяется требованием соблюдения условий параксиальности.

Так как при всех значениях углов и, лежащих в пределах апертуры параксиальных лучей, отношение а₂ /a₁, остается постоянным, то соотношение (6.1) показывает, что увеличение небольшого предмета А₁В₁ сохраняется неизменным, какой бы частью параксиального пучка ни было образовано изображение. Другими словами, изображение небольшого предмета, расположенного около оси, передается параксиальным пучком без искажения.

Для параксиальных лучей А₁ Р A₁S = a₁ и РА₂ SA₂ =a₂, так что

, ,

На основании (6.1) имеем

или

(6.2)

Соотношение (6.2) носит название теоремы Лагранжа — Гельмгольца.

Это соотношение справедливо для области параксиальных лучей. При употреблении пучков со значительной апертурой получение четких изображений возможно лишь при выполнении условия

y₁ n₁ sin u₁= y₂ n₂ sin u₂ (6.3)

(условие синусов Аббе). Условие Лагранжа — Гельмгольца или условие синусов налагает ограничение на свободу преобразования световых пучков при помощи оптических систем, связывая апертуру и размер предмета с апертурой и размером изображения. Из него вытекает, что преобразование данного оптического пучка при помощи оптической системы в другой пучок любого наперед заданного строения невозможно. Строение преобразованного пучка может быть только таким, какое допускает условие Лагранжа — Гельмгольца. Это важное принципиальное ограничение приобретает особое значение в вопросах фотометрии и концентрирования лучистой энергии при помощи оптических систем.