Преломление в линзе. Общая формула линзы

Большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал (обычно стекло) от окружающего воздуха. Такая система представляет, очевидно, обычную линзу.

Линза называется тонкой, если обе ее вершины можно считать совпадающими, т. е. если толщина линзы d мала по сравнению с R₁, и R₂, радиусами кривизны ограничивающих поверхностей. На рис. 8.1 для ясности линза изображена толстой. В дальнейших расчетах будем полагать, что точки S₁ и S₂ сливаются, и обозначим их буквой S. Все расстояния будем отсчитывать от этой точки S, которая практически совпадает с S₁ и S₂. Точка S носит название оптического центра линзы. Любой параксиальный луч, проходящий через S, практически не испытывает преломления. Действительно, для таких лучей участки обеих поверхностей диазы можно считать параллельными, так что луч, проходя через них, не меняет направления, но лишь смещается параллельно самому себе (преломление в плоскопараллельной пластинке), а так как толщиной линзы мы пренебрегаем, то смещение это ничтожно и луч практически проходит без преломления. Луч, проходящий через оптический центр, мы назовем осью линзы. Та из осей, которая проходит через центры обеих поверхностей, называется главной, остальные — побочными.

Преломление на первой сферической поверхности создало бы без второй сферической поверхности в сплошном стекле с показателем преломления п изображение С на расстоянии SC = а (см. рис. 8.1) от вершины, так что

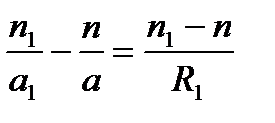
где а₁ = SA₁, R₁ — радиус кривизны первой поверхности линзы. Для второй поверхности С является как бы мнимым источником света. Построение изображения этого источника после преломления на второй поверхности линзы даст точку В на расстоянии а₂ = SB от линзы. Здесь опять применима формула:

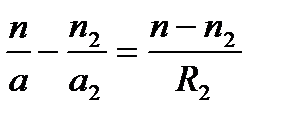
где R₂ — радиус второй поверхности.

Так как n₁ = n₂ (воздух с двух сторон линзы), то имеем:

,

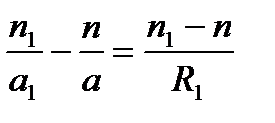Складывая второе уравнение с первым, получим:

,

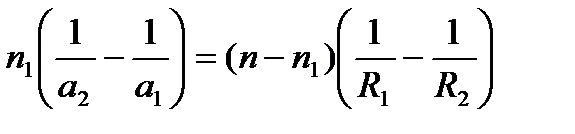или, вводя относительный показатель преломления N = п/п₁,

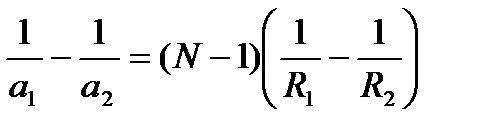
Эта общая формула линзы годна для линз выпуклых и вогнутых при любом расположении источника и соответствующем расположении фокуса. Нужно только принять во внимание знаки a₁, a₂, R₁, R₂ считая их положительными, если они отложены вправо от линзы, и отрицательными, если они отложены влево от линзы . Если знаки а₁ и а₂, одинаковы, то одна из сопряженных точек — мнимая, т. е. в ней пересекаются не сами лучи, а их воображаемые продолжения.

Если светящаяся точка, лежащая на главной оси, уделяется от линзы (а₁ возрастает по абсолютной величине), то изображение перемещается. Положение изображения, соответствующее предельному случаю, когда источник удален в бесконечность, носит название фокуса линзы. Таким образом, фокус есть точка, сопряженная бесконечно удаленной точке главной оси, или, что то же, — место схождения лучей, параллельных главной оптической оси. Расстояние от линзы до фокуса есть фокусное расстояние тонкой линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси, называется фокальной плоскостью. Если лучи идут из бесконечности параллельным пучком, но под углом к главной оси (вдоль побочной оси), то они пересекаются в соответствующей точке А фокальной плоскости. Таким образом, фокальная плоскость есть плоскость, сопряженная бесконечно удаленной плоскости.

Для определения фокусных расстояний имеем следующие соотношения:

при а₁= -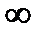

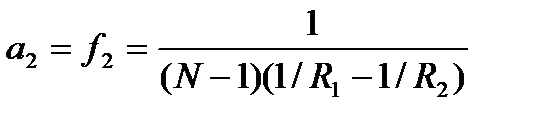
при а₂=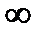

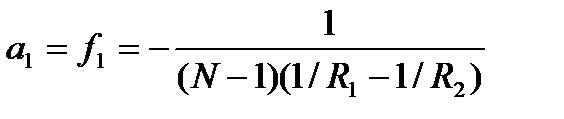
Итак, фокусные расстояния линзы равны по величине и противоположны по знаку, т.е. фокусы лежат по разные стороны от линзы.

В зависимости от знака и величины R₁ и R₂, а также от знака (N - 1), величина f₁ может быть положительной либо отрицательной, т. е. фокус может быть мнимым или действительным. То же относится и к f₂, причем нетрудно видеть, что если первый фокус — мнимый, то и второй будет мнимым, и наоборот.

Если фокусы действительны, т.е. параллельные лучи после преломления в линзе сходятся, то линза называется собирательной или положительной. При мнимых фокусах параллельные лучи после преломления в линзе становятся расходящимися. Поэтому такие линзы называются рассеивающими или отрицательными.