Фотометрические понятия и единицы

Воздействие света на глаз или какой-либо другой приемный аппарат состоит прежде всего в передаче этому регистрирующему аппарату энергии, переносимой световой волной. Поэтому, прежде чем рассматривать законы оптических явлений, мы должны составить себе представление об измерении света — фотометрии, которая сводится к измерению энергии, приносимой световой волной, или к измерению величин, так или иначе связанных с этой энергетической характеристикой. Прежде всего, необходимо дать определения тем величинам, которые фигурируют в измерительной практике. Их выбор обусловлен особенностями приемных аппаратов, непосредственно реагирующих на ту или иную из этих величин, а также возможностью осуществления эталонов для воспроизведения этих величин. При формулировке теоретических законов или практических выводов в разнообразных областях (теория излучения, светотехника, оптотехника, физиологическая оптика и т. д.) оказывается нередко удобным пользование то одними, то другими из введенных величин. Этим объясняется многообразие фотометрических понятий, к рассмотрению которых мы переходим.

а. Поток лучистой энергии Ф.

Представим себе источник света настолько малых размеров, что на некотором расстоянии от него можно считать поверхность распространяющейся волны сферической. Мы знаем, что такой источник обычно называют точечным.

Расположим на пути лучистой энергии, идущей от нашего источника L (рис. 4.1), какую-нибудь малую площадку σ и измерим количество энергии Q, протекающее через эту площадку за время τ. Для этой цели можно покрыть площадку веществом, поглощающим всю падающую энергию (сажа), и измерить поглощенную энергию например, по изменению температуры. Отношение

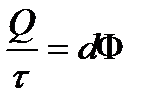
показывающее количество лучистой энергии, протекающей через площадку σ за единицу времени, т. е. мощность сквозь поверхность σ, называется потоком лучистой энергии через поверхность σ.

Так как лучистая энергия в однородной среде распространяется прямолинейно, то, проведя из точки L совокупность лучей, опирающихся на контур площадки σ, мы получим конус, ограничивающий часть потока, протекающую через σ. Если внутри среды поглощения энергии нет, то через любое сечение этого конуса протекает один и тот же поток. Сечение конуса сферической поверхностью с центром в L и с радиусом, равным единице, дает меру телесного угла конуса dΩ. Если нормаль п к поверхности σ составляет угол i с осью конуса, а расстояние от L до площадки есть R, то

Таким образом, выделенная нами часть потока приходится на телесный угол dΩ. При этом мы предполагаем, что линейные размеры площадки а малы по сравнению с R, так что dΩ — небольшая величина и внутри dΩ поток можно считать равномерным. Полный поток, идущий от L по всем направлениям, будет

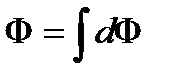
Поток есть основное понятие, необходимое для оценки количества энергии, проникающей в наши приборы. Знание потока существенно необходимо при расчете многих оптических устройств. Такой приемник, как, например, фотоэлемент, непосредственно реагирует на поток.

б. Сила света J.

Величину потока, приходящегося на единицу телесного угла, называют силой света. Если поток Ф посылается нашим источником равномерно по всем направлениям, то

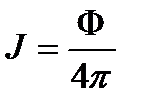
есть сила света, одинаковая для любого направления. В случае неравномерного потока величина Ф/4π представляет лишь среднюю силу света и называется средней сферической силой света. Для определения истинной силы света по какому-либо направлению надо выделить вдоль него достаточно малый элементарный телесный угол dΩ и измерить световой поток dФ, приходящийся на этот телесный угол.

Сила света по данному направлению определится соотношением

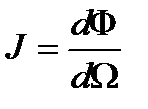
Охарактеризовав выбранное направление углами широты θ и долготы φ в некоторой полярной системе координат (рис. 4.2), можно обозначить силу света по данному направлению через J_θ,φ Величина эта есть функция φ и θ. Из рис. 4.2 явствует, что

dΩ=sin θdθdφ

и, следовательно, dΦ=J_θ,φsin θdθdφ, а полный поток

Если J не зависит от φ и θ (равномерный поток), то из этого общего соотношения следует, что

Ф=4πJ

Величина полного светового потока характеризует излучающий источник, и ее нельзя увеличить никакими оптическими системами. Действие этих систем может лишь сводиться к перераспределению светового потока, например, большей концентрации его по некоторым избранным направлениям. Таким способом достигается увеличение силы света по данным направлениям при соответствующем уменьшении ее по другим направлениям. Таково, например, действие сигнальных аппаратов пли прожекторов, позволяющих при помощи источников, обладающих средней сферической силой света в несколько сот кандел, создавать на оси прожектора силу света в миллионы кандел.

Для характеристики оптического излучения вводится ряд энер­гетических и фотометрических характеристик. Рассмотрим важ­нейшие из них.

В целом ряде измерений (например, астрономических) важно знать не только сам поток, но и поверхностную плотность потока излучения. Поверхностная плотность потока излучения равна отношению потока излучения к площади поверхности, через ко­торую проходит этот поток:

I_e=Ф_e/S = P/S=W/(St)

Часто эту величину называют облученностью и обозначают Е_е. Мы видим, что поверхностная плотность потока излучения определяется средним значением энергии, которую электромагнитная волна переносит через единицу площади в единицу времени.

Поэтому единица поверхностной плотности потока излучения — ватт на квадратный метр(Вт/м2) —поверхностная плот­ность такого потока излучения, при котором электромагнитная волна переносит через 1 м² поток излучения 1 Вт.

Представим себе, что через поверхность площадью S за время t волна переносит в среднем энергию, содержащуюся в па­раллелепипеде объемом V=St = S_ct.

В этом объеме полная энергия равна W=w_cpV, а поверхностная плотность потока излучения

I_e = w_cp_c

Термин «поверхностная плотность потока излучения» аналогичен термину интенсивность волны. В астрономии применяется термин светимость, который имеет аналогичный смысл и выражается в тех же единицах (Вт/м²).

Зависимость интенсивности волны от расстояния до источника и угла падения. Определим, как интенсивность волны зависит от расстояния точечного источника до облучаемой поверхности. Пусть точечный источник находится в центре двух концентри­ческих сфер радиусами R₁ и R₂.

Если среда не погло­щает (например, вакуум), то полная энергия, переносимая в еди­ницу времени через поверхностьи этих сфер, будет одной и той же. Поэтому

I₁=W/(4pR₁²t), I₂=W/(4pR₂²t),

откуда следует:

I₁/I₂=R₂²/R₁²

В астрономии расстояния до звезд определяют, сравнивая интенсивности их излучения (т.е. их светимости).

Для целого ряда практических случаев важна зависимость поверхностной плотности потока излучения от угла между направ­лением распространения волны и нормалью к освещаемой по­верхности.

Из рисунка следует, что через поверх­ности площадью S и S_o переносится волной одинаковая энергия. Поэтому I₀=W/(S_ot) и I=W/(St) и отношение интенсивностей

I/I₀=S₀/S=cosa,

откуда

I= I₀cosa.

Именно этой формулой и пользуются в большей части случаев для расчетов, ведь крайне редко поверхность расположена перпен­дикулярно световому потоку.

Наряду с энергетическими харак­теристиками важную роль в науке, технике и практической дея­тельности играют фотометрические характеристики, описывающие видимое излучение, т. е. ту часть спектра электромагнитных волн, которая воспринимается нашим глазом. Так, с потоком излучения непосредственно связана субъективная характеристика света — световой поток: мощность оптического излучения, оцени­ваемая по вызываемому им световому ощущению. Световой по­ток обозначается буквой Ф_v. Единицей светового потока в СИ служит люмен (лм).

Важнейшая характеристика любого источника света — сила света I_v. Она определяется отношением светового потока Ф_v к телесному углу W, внутри которого этот поток распространяется:

I_v = Ф_v/W.

Так как телесный угол вокруг точки равен 4p, то сила света точечного источника определяется из соотношения:

I_v = Ф_v/4p

В Международной системе единиц единица силы света — к а н д е л а (кд) — является основной. Кандела равна силе света в заданном направлении источника, испускающего монохрома­тическое излучение частотой 5,40*10¹⁴ Гц, энергетическая сила света которого в этом направлении составляет 1,683 Вт/ср. За­метим, что данная частота соответствует максимальной чувстви­тельности человеческого глаза, т. е. длине волны в вакууме, равной 555 нм.

Все остальные фотометрические единицы выражаются через канделу. Так, люмен равен световому потоку, испускаемому точечным источником силой света 1 кд в телесном угле, равном 1 ср.

Пусть на некоторую поверхность падает световой поток Ф₀. Очевидно, чем больше площадь этой поверхности, тем меньшая часть светового потока попадает на каждый участок, тем темнее этот участок. Освещенность E_v связывает световой поток с пло­щадью той поверхности, на которую этот поток падает. Освещен­ность в данной точке поверхности равна отношению светового потока, падающего на элемент поверхности, к площади этого элемента:

E_v = dФ_v/dS

Единица освещенности в СИ — л ю к с (лк) — равен освещен­ности поверхности площадью 1 м² при падающем на нее световом потоке 1 лм, равномерно распределенном по этой поверхности.

Выясним, от чего зависит освещен­ность поверхности, на которую падает световой поток. Прежде всего очевидно, что освещенность прямо пропорцио­нальна силе света источника. Ведь, чем больше сила света, тем больше световой поток, освещающий данную поверхность. Поэтому

E_v ~I_v

Но освещенность поверхности зависит не только от силы света источника, но и от расстояния до него. Пусть в центре сферы находится точечный источник, испускающий световой поток во все стороны. Площадь поверхности сферы равна 4πR², тогда полный световой поток Ф_v = 4πI_v Поэто­му выражение для освещенности имеет вид:

E_v=Ф_v/S=(4πI_v)/(4πR²)=I_v/R²

Значит, освещенность поверхности, создаваемая точечным ис­точником света, обратно пропорциональна квадрату расстояния от источника. Но в большин­стве случаев световой поток падает на освещаемую поверхность не перпендикулярно к ней, а под некоторым углом. Пусть свето­вой поток падает на элемент поверхности площадью DS, расположенный под углом j к направлению светового луча.

Площадь dS связана с площадью dS_o элемента сферической поверхности соотношением

dS₀ = dS cosj

Телесный угол

dW=dS_o/R²= dS cosj/R²