Понятие о когерентности

Закон независимости световых пучков, упомянутый ранее, означает, что световые пучки, встречаясь, не воздействуют друг на друга. Это положение было ясно сформулировано Гюйгенсом, который писал в своем «Трактате»: «Одно из чудеснейших свойств света состоит в том, что, когда он приходит из разных и даже противоположных сторон, лучи его производят свое действие, проходя один сквозь другой без всякой помехи. Этим вызывается то, что несколько зрителей могут одновременно видеть через одно и то же отверстие различные предметы ...». Сам Гюйгенс прибавляет, что этот вывод нетрудно понять с точки зрения волновых представлений. Он является следствием принципа суперпозиции, в силу которого световой вектор одной световой волны просто складывается с вектором другой полны, не испытывая никакого искажения. При этом, однако, возникает следующим вопрос. В силу принципа суперпозиции при сложении векторов отдельных ноли может получиться волна, амплитуда которой равна, например, сумме амплитуд складывающихся волн. А так как интенсивность волны пропорциональна квадрату амплитуды, то интенсивность результирующей волны не будет, вообще говоря, равна сумме интенсивностей складывающихся волн, ибо квадрат суммы нескольких величии не равен сумме их квадратов. Обычный же опыт показывает, что освещенность, создаваемая двумя или несколькими световыми пучками, представляется простой суммой освещенностей, создаваемых отдельными пучками. Таким образом, обычные экспериментальные факты кажутся на первый взгляд противоречащими волновым представлениям.

Для выяснения этой фундаментальной проблемы напомним сведения, относящиеся к сложению колебаний и волн.

При сложении двух гармонических колебаний одного периода

s₁ = a₁ sin (ωt+ φ₁) и s₂ = a₂ sin (ωt+ φ₂) (1.1)

происходящих по одному направлению, получится вновь гармоническое колебание того же периода

s = s₁+s₂ = A sin (ωt +θ), (1.2)

амплитуда А₁ и фаза θ которого определяются из следующих соотношений:

A²=a₁²+a₂²+2a₁a₂ cos(φ₁ – φ₂) (1.3)

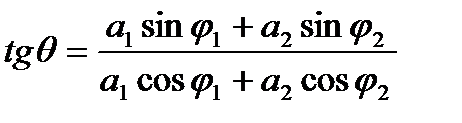
Выражение (1.3) показывает, что квадрат амплитуды результирующего колебания не равняется сумме квадратов амплитуд складывающихся колебаний, т. е. энергия результирующего колебания не равна сумме энергий складывающихся колебаний. Результат сложения зависит от разности фаз (φ₁ – φ₂ ) исходных колебаний и может иметь любое значение в пределах от А² = (а₁ — а₂)² (при φ₁ – φ₂ = π ) до А² = (а₁ + а₂)² (при φ₁ – φ₂ = 0).

Однако практически мы никогда не имеем дела со строго гармоническими колебаниями, описываемыми (1.1), т.е. колебаниями, длящимися бесконечно долго с неизменной амплитудой. Обычно колебания время от времени обрываются и возникают вновь уже с иной, нерегулярно измененной фазой, т. е. не являются строго гармоническими. В таком случае и результирующая интенсивность (I~A²) также меняется с течением времени.

Наблюдая эту интенсивность, мы могли бы получить изменяющиеся значения, однако для этого необходимо применить для наблюдения прибор, который реагировал бы достаточно быстро, чтобы отмечать изменения I. В противном случае мы не сможем следить за всеми изменениями I и будем регистрировать только некоторое , среднее по времени значение интенсивности I_ср, подобно тому, как глаз не в состоянии следить за колебаниями яркости лампочки накаливания, питаемой переменным током, и отмечает некоторую постоянную среднюю яркость.

Вводя обозначение ψ= φ₁ – φ₂ , вычислим средний квадрат амплитуды результирующего колебания за промежуток времени τ, длительный по сравнению с временем нерегулярных изменений фазы ψ.

I_ср~А_ср²=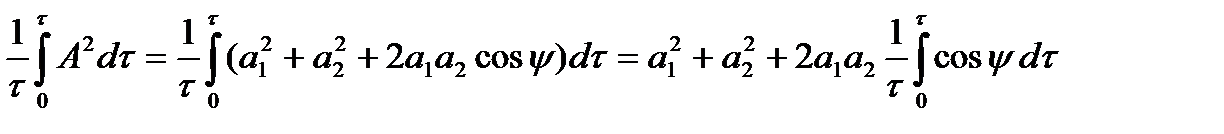

Если ψ остается неизменным в течение времени наблюдения τ, то

следовательно,

А_ср²= a₁²+a₂²+2a₁a₂ cos(φ₁ – φ₂), т.е. I_ср # I₁+I₂

При случайном же обрыве и возобновлении колебаний разность фаз изменяется совершенно беспорядочно, многократно пробегая за время τ все значения от нуля до 2π . Поэтому стремится к нулю, и мы имеем

А_ср²= a₁²+a₂², т.е. I_ср = I₁+I₂

Итак, при сложении двух колебаний одного периода надо различать два случая.

1. Разность фаз колебаний сохраняется неизменной за время τ, достаточное для наблюдений. Средняя энергия результирующего колебания отличается от суммы средних энергий исходных колебаний и может быть больше или меньше нее в зависимости от разности фаз. В этом случае колебания называются когерентными. Сложение колебаний, при котором не имеет места суммирование интенсивностей, мы будем называть интерференцией колебаний.

2. Разность фаз колебаний беспорядочно меняется за время наблюдения. Средняя энергия результирующего колебания равна сумме средних энергий исходных колебаний. Колебания в этом случае называются некогерентными. При их сложении всегда наблюдается суммирование интенсивностей, т. е. интерференция не имеет места.

Как указывалось выше, строго гармонические колебания одинаковой частоты всегда вполне когерентны между собой, ибо, поскольку они длятся, не обрываясь, имеющаяся у них разность фаз сохраняется без изменения сколь угодно долгое время. Поэтому при сложении таких гармонических колебаний всегда проявляется интерференция.

Итак, результат сложения двух гармонических колебаний одинаковой частоты зависит от соотношения между их фазами. При сложении большого числа N колебаний одинаковой частоты с произвольными фазами результат будет, конечно, зависеть от закона распределения фаз. Предполагая для простоты, что все колебания имеют одинаковые амплитуды, равные а, найдем, что результирующая интенсивность может заключаться между N²a² и нулем. Как показал Рэлей, при распределении фаз, которые подвергаются вполне случайным изменениям, средняя энергия суммы таких колебаний за время, охватывающее достаточно большое число изменений фаз, равна Na², т. е. в данном общем случае имеет место сложение интенсивностей. Этот вывод имеет самое непосредственное отношение к реальным источникам света. Результирующее колебание от отдельных испускающих центров (атомов), составляющих источник, создает освещенность, величина которой в данный момент и в данной точке зависит от соотношения фаз между колебаниями отдельных центров. Но наш глаз воспринимает лишь среднюю освещенность за некоторый достаточный для восприятия интервал времени и на некоторой достаточной по величине освещенной площадке. Это обстоятельство приводит к полному усреднению фазовых соотношений, в результате чего воспринимаемая освещенность окажется просто суммой освещенностей, создаваемых каждым светящимся центром нашего источника. Поэтому мы вправе сказать, что две одинаковые свечи дают освещенность вдвое большую, чем одна.